
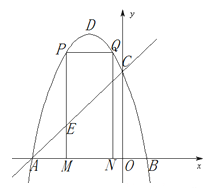
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=![]() DQ,求点F的坐标.
DQ,求点F的坐标.
【答案】(1)A(-3,0),B(1,0),C(0,3); (2)![]() ;(3)
;(3)![]() 或(1,0).
或(1,0).
【解析】
试题(1)通过解析式即可得出C点坐标,令y=0,解方程得出方程的解,即可求得A、B的坐标;
(2)设M点横坐标为m,则PM=![]() ,MN=(﹣m﹣1)×2=﹣2m﹣2,矩形PMNQ的周长d=
,MN=(﹣m﹣1)×2=﹣2m﹣2,矩形PMNQ的周长d=![]() ,将
,将![]() 配方,由二次函数的性质,即可得出m的值,然后求得直线AC的解析式,把x=m代入可以求得三角形的边长,从而求得三角形的面积;
配方,由二次函数的性质,即可得出m的值,然后求得直线AC的解析式,把x=m代入可以求得三角形的边长,从而求得三角形的面积;
(3)设F(n,![]() ),由已知若FG=
),由已知若FG=![]() DQ,即可求得.
DQ,即可求得.
试题解析:解:(1)由抛物线![]() 可知,C(0,3),令y=0,则
可知,C(0,3),令y=0,则![]() ,解得x=﹣3或x=1,∴A(﹣3,0),B(1,0);
,解得x=﹣3或x=1,∴A(﹣3,0),B(1,0);
(2)由抛物线![]() 可知,对称轴为x=﹣1,设M点的横坐标为m,则PM=
可知,对称轴为x=﹣1,设M点的横坐标为m,则PM=![]() ,MN=(﹣m﹣1)×2=﹣2m﹣2,∴矩形PMNQ的周长=2(PM+MN)=(
,MN=(﹣m﹣1)×2=﹣2m﹣2,∴矩形PMNQ的周长=2(PM+MN)=(![]() )×2=
)×2=![]() =
=![]() ,∴当m=﹣2时矩形的周长最大.∵A(﹣3,0),C(0,3),设直线AC解析式为y=kx+b,解得k=1,b=3,∴解析式y=x+3,当x=﹣2时,则E(﹣2,1),∴EM=1,AM=1,∴S=
,∴当m=﹣2时矩形的周长最大.∵A(﹣3,0),C(0,3),设直线AC解析式为y=kx+b,解得k=1,b=3,∴解析式y=x+3,当x=﹣2时,则E(﹣2,1),∴EM=1,AM=1,∴S=![]() AMEM=
AMEM=![]() ;
;
(3)∵M点的横坐标为﹣2,抛物线的对称轴为x=﹣1,∴N应与原点重合,Q点与C点重合,∴DQ=DC,把x=﹣1代入![]() ,解得y=4,∴D(﹣1,4),∴DQ=DC=
,解得y=4,∴D(﹣1,4),∴DQ=DC=![]() ,∵FG=
,∵FG=![]() DQ,∴FG=4,设F(n,
DQ,∴FG=4,设F(n,![]() ),则G(n,n+3),∵点G在点F的上方,∴
),则G(n,n+3),∵点G在点F的上方,∴![]() =4,解得:n=﹣4或n=1,∴F(﹣4,﹣5)或(1,0).
=4,解得:n=﹣4或n=1,∴F(﹣4,﹣5)或(1,0).


科目:初中数学 来源: 题型:
【题目】班级元旦晚会上,主持人给大家带来了一个有奖竞猜题,他在一个不透明的袋子中放了若干个形状大小完全相同的白球,想请大家想办法估计出袋中白球的个数.数学课代表小明是这样来估计的:他先往袋中放入10个形状大小与白球相同的红球,混匀后再从袋子中随机摸出20个球,发现其中有4个红球.如果设袋中有白球x个,根据小明的方法用来估计袋中白球个数的方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知:a=![]() ﹣2,b=
﹣2,b=![]() +2,求代数式a2b﹣ab2的值;
+2,求代数式a2b﹣ab2的值;
(2)已知实数x、y满足x2+10x+![]() +25=0,则(x+y)2019的值是多少?
+25=0,则(x+y)2019的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线l:y=﹣![]() x+6交y轴于点A,与x轴交于点B,过A、B两点的抛物线m与x轴的另一个交点为C,(C在B的左边),如果BC=5,求抛物线m的解析式,并根据函数图像指出当m的函数值大于0的函数值时x的取值范围.
x+6交y轴于点A,与x轴交于点B,过A、B两点的抛物线m与x轴的另一个交点为C,(C在B的左边),如果BC=5,求抛物线m的解析式,并根据函数图像指出当m的函数值大于0的函数值时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x的一次函数,且当x=-4,y=9;当x=6时,y=-1.
(1)求这个一次函数的解析式和自变量x的取值范围;
(2)当x=-![]() 时,函数y的值;
时,函数y的值;
(3)当y=7时,自变量x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】前年甲厂全年的产值比乙厂多12万元,在其后的两年内,两个厂的产值都有所增加:甲厂每年的产值比上一年递增10万元,而乙厂每年的产值比上一年增加相同的百分数.去年甲厂全年的产值仍比乙厂多6万元,而今年甲厂全年产值反而比乙厂少3.2万元.前年甲乙两车全年的产值分别是多少?乙厂每年的产值递增的百分数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
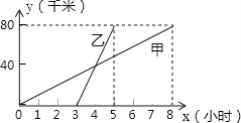
【题目】如图,甲、乙两人分别骑自行车和摩托车沿相同路线由A地到B地,行驶过程中的函数图象如图所示,请根据图象回答下列问题:
(1)______先出发,提前______小时;
(2)______先到达B地,早到______小时;
(3)A地与B地相距______千米;
(4)甲乙两人在途中的速度分别是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com