练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知y是x的一次函数，且当x=-4，y=9；当x=6时，y=-1．

    （1）求这个一次函数的解析式和自变量x的取值范围；

    （2）当x=-时，函数y的值；

    （3）当y=7时，自变量x的值．

    【答案】（1）一次函数的解析式为y=-x+5，自变量x的取值范围是x取任意实数；（2）5.5；（3）x=-2

    【解析】

    （1）设y=kx+b，代入（-4，9）和（6，-1）得关于k和b的方程组，解方程组即可；

    （2）代入x=-于函数式中即可求出y值；

    （3）把y=7代入函数式，即可求解x的值．

    解：（1）设y=kx+b，

    代入（-4，9）和（6，-1）得，

    解得k=-1，b=5，

    所以一次函数的解析式为y=-x+5，自变量x的取值范围是：x取任意实数；

    （2）当x=-时，y=-（-）+5=5.5；

    （3）当y=7时，即7=-x+5，

    解得x=-2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读材料：

    如果两个正数a，b，即a＞0，b＞0，则有下面的不等式： ，当且仅当a＝b时取等号，我们把叫做正数a，b的算术平均数，把叫做正数a，b的几何平均数，于是上述的不等式可以表述为：两个正数的算术平均数不小于（即大于或等于）他们的几何平均数．它在数学中有广泛的应用，是解决最大（小）值问题的有力工具．

    实例剖析：

    已知x＞0，求式子的最小值．

    解：令a＝x，b＝，则由，得当且仅当时，方程两边同时乘x，得到，解得x＝2，式子有最小值，最小值为4．

    学以致用：

    根据上面的阅读材料回答下列问题：

    （1）已知x＞0，则当x＝__________时，式子取到最小值，最小值为：_______________

    （2）用篱笆围一个面积为100m的长方形花园，问这个长方形的长、宽各为多少时，所用的篱笆最短，最短的篱笆是多少米？

    （3）已知x＞0，则x取何值时，式子取到最小值，最小值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，E、F分别是边AB、BC的中点，连接AF、DE相交于点G，连接CG．

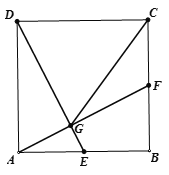
    （1）求证：AF⊥DE；

    （2）求证：CG=CD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

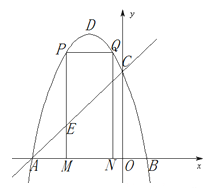
    【题目】如图，抛物线的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点.

    （1）求A、B、C的坐标；

    （2）点M为线段AB上一点（点M不与点A、B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N.若点P在点Q左边，当矩形PQMN的周长最大时，求△AEM的面积；

    （3）在（2）的条件下，当矩形PMNQ的周长最大时，连接DQ.过抛物线上一点F作y轴的平行线，与直线AC交于点G（点G在点F的上方）.若FG=DQ，求点F的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知二次函数y=x2+x1的图象与x轴交于A、B两点，与y轴交于点C，连接AC，点P是抛物线上的一个动点，记△APC的面积为S，当S=2时，相应的点P的个数是______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某项研究表明，大拇指与小拇指尽量张开时，两指尖的距离称为指距．如表是测得的指距与身高的一组数据：

    指距d（cm）

    19

    20

    21

    身高h（cm）

    151

    160

    169

    （1）你能确定身高h与指距d之间的函数关系式吗？

    （2）若某人的身高为196cm，一般情况下他的指距应是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在平面直角坐标系中，直线AB与轴交于点A，与轴交于点B，与直线OC：交于点C．

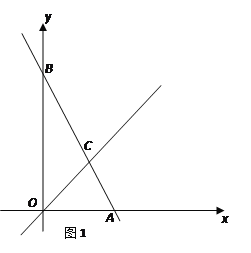
    （1）若直线AB解析式为，

    ①求点C的坐标；

    ②求△OAC的面积．

    （2）如图2，作的平分线ON，若AB⊥ON，垂足为E， OA＝4，P、Q分别为线段OA、OE上的动点，连结AQ与PQ，试探索AQ＋PQ是否存在最小值？若存在，求出这个最小值；若不存在，说明理由．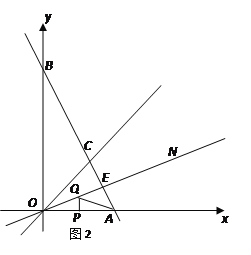

    查看答案和解析>>

    科目：初中数学 来源： 题型：

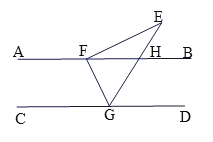
    【题目】如图，AB// CD，Rt△EFG的顶点F，G分别落在直线AB，CD上，GE交AB于点H，∠EFG=90°，∠E=32°．

    （1）∠FGE=　　　　°

    （2）若GE平分∠FGD，求∠EFB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平行四边形ABCD中，AB＜BC．

    （1）利用尺规作图，在AD边上确定点E，使点E到边AB，BC的距离相等（不写作法，保留作图痕迹）；

    （2）若BC=8，CD=5，则DE= ．

    查看答案和解析>>

    同步练习册答案