
【题目】阅读材料:
如果两个正数a,b,即a>0,b>0,则有下面的不等式: ![]() ,当且仅当a=b时取等号,我们把
,当且仅当a=b时取等号,我们把![]() 叫做正数a,b的算术平均数,把
叫做正数a,b的算术平均数,把![]() 叫做正数a,b的几何平均数,于是上述的不等式可以表述为:两个正数的算术平均数不小于(即大于或等于)他们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具.
叫做正数a,b的几何平均数,于是上述的不等式可以表述为:两个正数的算术平均数不小于(即大于或等于)他们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具.
实例剖析:
已知x>0,求式子![]() 的最小值.
的最小值.
解:令a=x,b=![]() ,则由
,则由![]() ,得
,得![]() 当且仅当
当且仅当![]() 时,方程两边同时乘x,得到
时,方程两边同时乘x,得到![]() ,解得x=2,式子有最小值,最小值为4.
,解得x=2,式子有最小值,最小值为4.
学以致用:
根据上面的阅读材料回答下列问题:
(1)已知x>0,则当x=__________时,式子![]() 取到最小值,最小值为:_______________
取到最小值,最小值为:_______________
(2)用篱笆围一个面积为100m的长方形花园,问这个长方形的长、宽各为多少时,所用的篱笆最短,最短的篱笆是多少米?
(3)已知x>0,则x取何值时,式子![]() 取到最小值,最小值是多少?
取到最小值,最小值是多少?
【答案】(1) ![]() ,
,![]() ;(2) 当矩形的长、宽各为10米时,所用篱笆最短,最短为40米;(3) 当x=3时,y取得最小值为4.
;(2) 当矩形的长、宽各为10米时,所用篱笆最短,最短为40米;(3) 当x=3时,y取得最小值为4.
【解析】
(1)令a=2x,b=![]() ,这两个数都是正数,根据阅读材料
,这两个数都是正数,根据阅读材料![]() 就可以直接得到结果;
就可以直接得到结果;
(2)设这个矩形的长为x米,则宽=面积÷长,即宽为![]() 米,则所用的篱笆长等于长加宽的和乘以2,根据阅读材料即可求解;
米,则所用的篱笆长等于长加宽的和乘以2,根据阅读材料即可求解;
(3)将原式整理成![]() ,根据阅读材料直接求解最小值即可.
,根据阅读材料直接求解最小值即可.
解:(1)令a=2x,b=![]() ,
,
已知![]() ,
,
则![]() ,
,
当且仅当![]() 时,即
时,即![]() ,式子有最小值.
,式子有最小值.
(2) 设这个矩形的长为x米,所用篱笆的长度为y米,
根据题意得:![]() ,
,
由上述性质可知:
∵![]() ,
,
∴![]() ,
,
此时![]() ,
,
解得:x=10,
∴当矩形的长、宽各为10米时,所用篱笆最短,最短为40米.
(3) ![]() ,
,
![]() ,
,
当![]() 时,y取得最小值为4,
时,y取得最小值为4,
∴当x=3时,y取得最小值为4.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴于(﹣1,0)、(3,0)两点,以下四个结论正确的是(用序号表示)______________.
(1)图象的对称轴是直线 x=1
(2)当x>1时,y随x的增大而减小
(3)一元二次方程ax2+bx+c=0的两个根是﹣1和3
(4)当﹣1<x<3时,y<0.
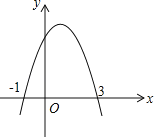
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】班级元旦晚会上,主持人给大家带来了一个有奖竞猜题,他在一个不透明的袋子中放了若干个形状大小完全相同的白球,想请大家想办法估计出袋中白球的个数.数学课代表小明是这样来估计的:他先往袋中放入10个形状大小与白球相同的红球,混匀后再从袋子中随机摸出20个球,发现其中有4个红球.如果设袋中有白球x个,根据小明的方法用来估计袋中白球个数的方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
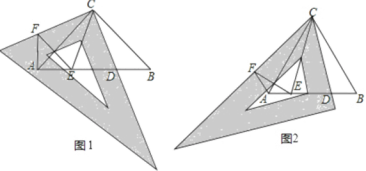
【题目】(1)如图1,△ABC为等腰直角三角形,∠ACB=90°,先将三角板的90°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于45°).旋转后三角板的一直角边与AB交于点D.在三角板另一直角边上取一点F,使CF=CD,线段AB上取点E,使∠DCE=45°,连接AF,EF.请探究结果:
①直接写出∠EAF的度数=__________度;若旋转角∠BCD=α°,则∠AEF=____________度(可以用含α的代数式表示);
②DE与EF相等吗?请说明理由;
(类比探究)
(2)如图2,△ABC为等边三角形,先将三角板中的60°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于30°).旋转后三角板的一直角边与AB交于点D.在三角板斜边上取一点F,使CF=CD,线段AB上取点E,使∠DCE=30°,连接AF,EF.
①直接写出∠EAF的度数=___________度;
②若AE=1,BD=2,求线段DE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
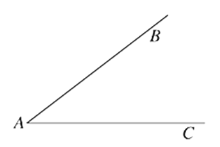
在数学课上,老师提出如下问题:尺规作图:作已知角的角平分线.已知:如图,∠BAC.求作:∠BAC的角平分线AP.
小欣的作法如下:
(1)如图,在平面内任取一点O;
(2)以点O为圆心,AO为半径作圆,交射线AB于点D,交射线AC于点E;
(3)连接DE,过点O作射线OP垂直于线段DE,交⊙O于点P;
(4)过点P作射线AP.
所以射线AP为所求
根据小欣设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵OP![]() DE
DE
∴ ![]() =______(________________________)(填推理的依据),
=______(________________________)(填推理的依据),
∴∠BAP=______ (________________________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知:a=![]() ﹣2,b=
﹣2,b=![]() +2,求代数式a2b﹣ab2的值;
+2,求代数式a2b﹣ab2的值;
(2)已知实数x、y满足x2+10x+![]() +25=0,则(x+y)2019的值是多少?
+25=0,则(x+y)2019的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x的一次函数,且当x=-4,y=9;当x=6时,y=-1.
(1)求这个一次函数的解析式和自变量x的取值范围;
(2)当x=-![]() 时,函数y的值;
时,函数y的值;
(3)当y=7时,自变量x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com