
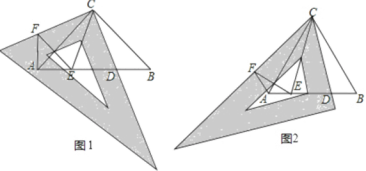
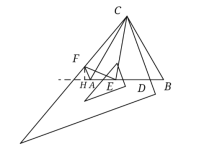
【题目】(1)如图1,△ABC为等腰直角三角形,∠ACB=90°,先将三角板的90°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于45°).旋转后三角板的一直角边与AB交于点D.在三角板另一直角边上取一点F,使CF=CD,线段AB上取点E,使∠DCE=45°,连接AF,EF.请探究结果:
①直接写出∠EAF的度数=__________度;若旋转角∠BCD=α°,则∠AEF=____________度(可以用含α的代数式表示);
②DE与EF相等吗?请说明理由;
(类比探究)
(2)如图2,△ABC为等边三角形,先将三角板中的60°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于30°).旋转后三角板的一直角边与AB交于点D.在三角板斜边上取一点F,使CF=CD,线段AB上取点E,使∠DCE=30°,连接AF,EF.
①直接写出∠EAF的度数=___________度;
②若AE=1,BD=2,求线段DE的长度.
【答案】(1)①90,2α;②相等,理由见解析;(2)①120;②![]() .
.
【解析】
(1)①等腰直角三角形的性质可得出AC=BC,∠BAC=∠B=45°,证出∠ACF=∠BCD,由SAS证明出△ACF≌△BCD,得出∠CAF=∠B=45°,AF=DB,即可求解;②证出∠FCE=∠ECD即可证明△CFE≌△CDE,得出EF=DE,∠CFE=∠CDE,从而求出题①中∠AFE的度数;
(2)①由△ABC是等边三角形得出AC=BC,∠BAC=∠B=60°,求出∠ACF=∠BCD,,证明出△ACF≌△BCD,得出∠CAF=∠B=60°即可求解;②证出∠DCE=∠FCE,由SAS证明△CFE≌△CDE,得出DE=EF,作FH⊥AE交EA的延长线于点H,解直角三角形即可求解.
解:(1)①∵△ABC是等腰直角三角形,∠ACB=90°,
∴AC=BC,∠BAC=∠B=45°,
∵∠DCF=90°,
∴∠ACF=∠BCD,
在△ACF和△BCD中
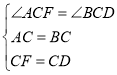
∴△ACF≌△BCD(SAS),
∴∠CAF=∠B=45°,AF=DB,
∴∠EAF=∠BAC+∠CAF=90°.
②相等
∵∠ECD=45°,∠FCD=90°,
∴∠FCE=∠ECD =45°,
在△CFE和△CDE中
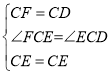
△CFE≌△CDE(SAS),
∴EF=DE,∠CFE=∠CDE,
∵∠CDE=∠B+α°=45°+α°,
∴∠EFC=45°+α°,
∴∠EFC+∠AFE=∠CDB=180°-45°-α,
∴45°+α°+∠AFE=135°-α°,
∴2α°=90°-∠AFE=∠AFE,
∴∠AFE=2α°.
(2)①∵△ABC是等边三角形,
∴AC=BC,∠BAC=∠B=60°,
又∵∠DCF=60°
∴∠ACF=∠BCD,
在△ACF和△BCD中
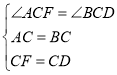
∴△ACF≌△BCD(SAS),
∴∠CAF=∠B=60°,
∴∠EAF=∠CAF+∠CAE=120°.
②作FH⊥AE交EA的延长线于点H,如图所示,
∵∠DCF=60°,∠DCE=30°,
∴∠FCE=30°,
∴∠FCE=∠DCE,
在△CFE和△CDE中
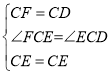
△CFE≌△CDE(SAS),
∴DE=EF,
在Rt△AFH中
∵∠AFH=180°-120°=60°,
∴AF=BD=2,
∴AH=1,FH=![]() ,
,
在Rt△EFH中,EF=![]() ,
,
∴EF=DE=![]() .
.


科目:初中数学 来源: 题型:
【题目】某商品交易会上,一商人将每件进价为 5 元的纪念品,按每件 9 元出售,每天可售出 32件.他想采用提高售价的办法来增加利润,经试验,发现这种纪念品每件提价 2 元,每天的销售量会减少 8 件.
(1)当售价定为多少元时,每天的利润为 140 元?
(2)写出每天所得的利润 y(元)与售价 ![]() (元/件)之间的函数关系式,每件售价定为多少元,才能使一天所得的利润最大?最大利润是多少元?(利润=(售价-进价)×售出件数)
(元/件)之间的函数关系式,每件售价定为多少元,才能使一天所得的利润最大?最大利润是多少元?(利润=(售价-进价)×售出件数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数![]() (x>0)的图象上,点C,D在反比例函数
(x>0)的图象上,点C,D在反比例函数![]() (k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为( )
,则k的值为( )
A. 3 B. 4 C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
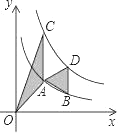
【题目】在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)先作△ABC关于原点O成中心对称的![]() ,再把
,再把![]() 向上平移4个单位长度得到
向上平移4个单位长度得到![]() ;
;
(2)△ABC可以经过一次旋转变换得到![]() ,旋转角的大小为多少?写出旋转中心的坐标.
,旋转角的大小为多少?写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
如果两个正数a,b,即a>0,b>0,则有下面的不等式: ![]() ,当且仅当a=b时取等号,我们把
,当且仅当a=b时取等号,我们把![]() 叫做正数a,b的算术平均数,把
叫做正数a,b的算术平均数,把![]() 叫做正数a,b的几何平均数,于是上述的不等式可以表述为:两个正数的算术平均数不小于(即大于或等于)他们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具.
叫做正数a,b的几何平均数,于是上述的不等式可以表述为:两个正数的算术平均数不小于(即大于或等于)他们的几何平均数.它在数学中有广泛的应用,是解决最大(小)值问题的有力工具.
实例剖析:
已知x>0,求式子![]() 的最小值.
的最小值.
解:令a=x,b=![]() ,则由
,则由![]() ,得
,得![]() 当且仅当
当且仅当![]() 时,方程两边同时乘x,得到
时,方程两边同时乘x,得到![]() ,解得x=2,式子有最小值,最小值为4.
,解得x=2,式子有最小值,最小值为4.
学以致用:
根据上面的阅读材料回答下列问题:
(1)已知x>0,则当x=__________时,式子![]() 取到最小值,最小值为:_______________
取到最小值,最小值为:_______________
(2)用篱笆围一个面积为100m的长方形花园,问这个长方形的长、宽各为多少时,所用的篱笆最短,最短的篱笆是多少米?
(3)已知x>0,则x取何值时,式子![]() 取到最小值,最小值是多少?
取到最小值,最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
为了响应“十三五”规划中提出的绿色环保的倡议,某校文印室提出了每个人都践行“双面打印,节约用纸”.已知打印一份资料,如果用A4厚型纸单面打印,总质量为400克,将其全部改成双面打印,用纸将减少一半;如果用A4薄型纸双面打印,这份资料的总质量为160克,已知每页薄型纸比厚型纸轻0.8克,求A4薄型纸每页的质量.(墨的质量忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AC是菱形ABCD的对角线,且AC=BC.
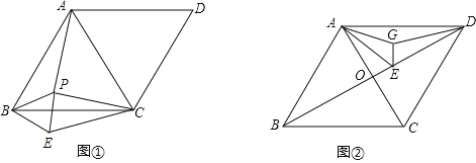
(1)如图①,点P是△ABC的一个动点,将△ABP绕着点B旋转得到△CBE.
①求证:△PBE是等边三角形;
②若BC=5,CE=4,PC=3,求∠PCE的度数;
(2)连结BD交AC于点O,点E在OD上且DE=3,AD=4,点G是△ADE内的一个动点如图②,连结AG,EG,DG,求AG+EG+DG的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
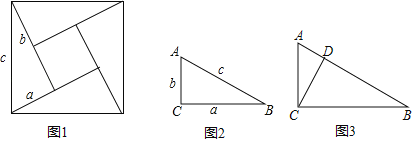
【题目】如图1所示,有四个同样大小的直角三角形,两条直角边分别为a、b,斜边为c,拼成一个正方形,中间留有一个小正方形.
(1)利用它们之间的面积关系,探索出关于a、b、c的等式;
(2)利用(1)中发现的直角三角形中两直角边a,b和斜边c之间的关系,完成问题:如图2,在直角△ABC中,∠C=90°,且c=6,a+b=8,则△ABC的面积为 ;
(3)如图3所示,CD是直角△ABC中斜边上的高,试证明CD2=ADBD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某项研究表明,大拇指与小拇指尽量张开时,两指尖的距离称为指距.如表是测得的指距与身高的一组数据:
指距d(cm) | 19 | 20 | 21 |
身高h(cm) | 151 | 160 | 169 |
(1)你能确定身高h与指距d之间的函数关系式吗?
(2)若某人的身高为196cm,一般情况下他的指距应是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com