
【题目】已知:AC是菱形ABCD的对角线,且AC=BC.
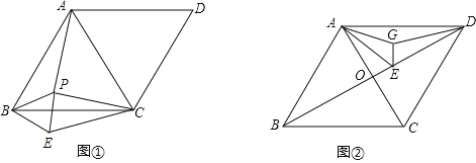
(1)如图①,点P是△ABC的一个动点,将△ABP绕着点B旋转得到△CBE.
①求证:△PBE是等边三角形;
②若BC=5,CE=4,PC=3,求∠PCE的度数;
(2)连结BD交AC于点O,点E在OD上且DE=3,AD=4,点G是△ADE内的一个动点如图②,连结AG,EG,DG,求AG+EG+DG的最小值.
【答案】(1)①见解析,②∠PCE=30°;(2)AG+EG+DG的最小值为5.
【解析】
(1)①先判断出△ABC等边三角形,得出∠ABC=60°,再由旋转知BP=BE,∠PBE=∠ABC=60°,即可得出结论.
②先用勾股定理的逆定理判断出△ACP是直角三角形,得出∠APC=90°,进而判断出∠PBE+∠PCE=90°,即可得出结论;
(2)先判断出△G'DG是等边三角形,得出GG'=DG,即:AG+EG+DG=A'G'+EG+GG'得出当A'、G'、G、E四点共线时,A'G'+EG+G'G的值最小,即可得出结论.
解:(1)①∵四边形ABCD是菱形
∴AB=BC,
∵AC=BC,
∴AB=BC=AC,
∴△ABC等边三角形,
∴∠ABC=60°,
由旋转知BP=BE,∠CBE=∠ABP
∴∠CBE+∠PBC=∠ABP+∠PBC
∴∠PBE=∠ABC=60°,
∴△PBE是等边三角形;
②由①知AB=BC=5
∵由旋转知△ABP≌△CBE,
∴AP=CE=4,∠APB=∠BEC,
∵AP2+PC2=42+32=25=AC2,
∴△ACP是直角三角形,
∴∠APC=90°,
∴∠APB+∠BPC=270°,
∵∠APB=∠CEB,
∴∠CEB+∠BPC=270°,
∴∠PBE+∠PCE=360°-(∠CEB+∠BPC)=90°,
∵∠PBE=∠ABC=60°,
∴∠PCE=90°-60°=30°;
(2)如图,将△ADG绕着点D顺时针旋转60°得到△A'DG',
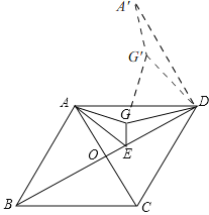
由旋转知△ADG≌△A'DG',
∴A'D=AD=4,G'D=GD,A'G'=AG,
∵∠G'DG=60°,G'D=GD,
∴△G'DG是等边三角形,
∴GG'=DG,
∴AG+EG+DG=A'G'+EG+GG'
∵当A'、G'、G、E四点共线时,A'G'+EG+G'G的值最小,
即AG+EG+DG的值最小,
∵∠A'DA=60°,∠ADE=![]() ∠ADC=30°,
∠ADC=30°,
∴∠A'DE=90°,
∴AG+EG+DG=A'G'+EG+G'G=A'E=![]() =5,
=5,
∴AG+EG+DG的最小值为5.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
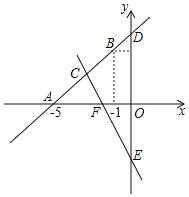
【题目】如图,直线y=kx+b经过点A(-5,0),B(-1,4)
(1)求直线AB的表达式;
(2)求直线CE:y=-2x-4与直线AB及y轴围成图形的面积;
(3)根据图象,直接写出关于x的不等式kx+b>-2x-4的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】班级元旦晚会上,主持人给大家带来了一个有奖竞猜题,他在一个不透明的袋子中放了若干个形状大小完全相同的白球,想请大家想办法估计出袋中白球的个数.数学课代表小明是这样来估计的:他先往袋中放入10个形状大小与白球相同的红球,混匀后再从袋子中随机摸出20个球,发现其中有4个红球.如果设袋中有白球x个,根据小明的方法用来估计袋中白球个数的方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,△ABC为等腰直角三角形,∠ACB=90°,先将三角板的90°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于45°).旋转后三角板的一直角边与AB交于点D.在三角板另一直角边上取一点F,使CF=CD,线段AB上取点E,使∠DCE=45°,连接AF,EF.请探究结果:
①直接写出∠EAF的度数=__________度;若旋转角∠BCD=α°,则∠AEF=____________度(可以用含α的代数式表示);
②DE与EF相等吗?请说明理由;
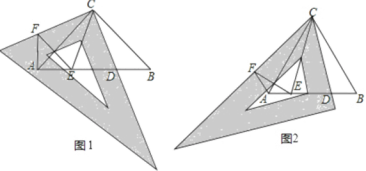
(类比探究)
(2)如图2,△ABC为等边三角形,先将三角板中的60°角与∠ACB重合,再将三角板绕点C按顺时针方向旋转(旋转角大于0°且小于30°).旋转后三角板的一直角边与AB交于点D.在三角板斜边上取一点F,使CF=CD,线段AB上取点E,使∠DCE=30°,连接AF,EF.
①直接写出∠EAF的度数=___________度;
②若AE=1,BD=2,求线段DE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:尺规作图:作已知角的角平分线.已知:如图,∠BAC.求作:∠BAC的角平分线AP.
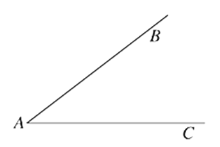
小欣的作法如下:
(1)如图,在平面内任取一点O;
(2)以点O为圆心,AO为半径作圆,交射线AB于点D,交射线AC于点E;
(3)连接DE,过点O作射线OP垂直于线段DE,交⊙O于点P;
(4)过点P作射线AP.
所以射线AP为所求
根据小欣设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵OP![]() DE
DE
∴ ![]() =______(________________________)(填推理的依据),
=______(________________________)(填推理的依据),
∴∠BAP=______ (________________________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填幻方:将1、2、3、4、5、6、7、8、9这九个数字分别填在如图所示的九个空格中,要求每一行从左到右的数字逐渐增大,每一列从上到下的数字也逐渐增大.当数字2、4固定在图中所示的位置时,按规则填写空格,所有可能出现的结果有( )
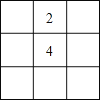
A.4种B.6种C.8种D.9种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知:a=![]() ﹣2,b=
﹣2,b=![]() +2,求代数式a2b﹣ab2的值;
+2,求代数式a2b﹣ab2的值;
(2)已知实数x、y满足x2+10x+![]() +25=0,则(x+y)2019的值是多少?
+25=0,则(x+y)2019的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线l:y=﹣![]() x+6交y轴于点A,与x轴交于点B,过A、B两点的抛物线m与x轴的另一个交点为C,(C在B的左边),如果BC=5,求抛物线m的解析式,并根据函数图像指出当m的函数值大于0的函数值时x的取值范围.
x+6交y轴于点A,与x轴交于点B,过A、B两点的抛物线m与x轴的另一个交点为C,(C在B的左边),如果BC=5,求抛物线m的解析式,并根据函数图像指出当m的函数值大于0的函数值时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】前年甲厂全年的产值比乙厂多12万元,在其后的两年内,两个厂的产值都有所增加:甲厂每年的产值比上一年递增10万元,而乙厂每年的产值比上一年增加相同的百分数.去年甲厂全年的产值仍比乙厂多6万元,而今年甲厂全年产值反而比乙厂少3.2万元.前年甲乙两车全年的产值分别是多少?乙厂每年的产值递增的百分数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com