
【题目】如图,在正方形ABCD中,E、F分别是边AB、BC的中点,连接AF、DE相交于点G,连接CG.
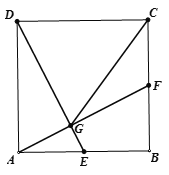
(1)求证:AF⊥DE;
(2)求证:CG=CD.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题(1)正方形ABCD中,AB=BC,BF=AE,且∠ABF=∠DAE=90°,即可证明△ABF≌△DAE,即可得∠DGA=90°,结论成立.
(2)延长AF交DC延长线于M,证明△ABF≌△MCF,说明△DGM是直角三角形,命题得证.
试题解析:(1)∵四边形ABCD为正方形
∴AB=BC=CD=AD,∠ABF=∠DAE=90°,
又∵E,F分别是边AB.BC的中点
∴AE=![]() AB.BF=
AB.BF=![]() BC
BC
∴AE=BF.
在△ABF与△DAE中,
 ,
,
∴△DAE≌△ABF(SAS).
∴∠ADE=∠BAF,
∵∠BAF+∠DAG=90°,
∴∠ADG+∠DAG=90°,
∴∠DGA=90°,即AF⊥DE.
(2)证明:延长AF交DC延长线于M,

∵F为BC中点,
∴CF=FB
又∵DM∥AB,
∴∠M=∠FAB.
在△ABF与△MCF中,

∴△ABF≌△MCF(AAS),
∴AB=CM.
∴AB=CD=CM,
∵△DGM是直角三角形,
∴GC=![]() DM=DC.
DM=DC.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出如下问题:尺规作图:作已知角的角平分线.已知:如图,∠BAC.求作:∠BAC的角平分线AP.
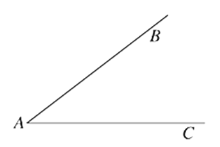
小欣的作法如下:
(1)如图,在平面内任取一点O;
(2)以点O为圆心,AO为半径作圆,交射线AB于点D,交射线AC于点E;
(3)连接DE,过点O作射线OP垂直于线段DE,交⊙O于点P;
(4)过点P作射线AP.
所以射线AP为所求
根据小欣设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵OP![]() DE
DE
∴ ![]() =______(________________________)(填推理的依据),
=______(________________________)(填推理的依据),
∴∠BAP=______ (________________________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知:a=![]() ﹣2,b=
﹣2,b=![]() +2,求代数式a2b﹣ab2的值;
+2,求代数式a2b﹣ab2的值;
(2)已知实数x、y满足x2+10x+![]() +25=0,则(x+y)2019的值是多少?
+25=0,则(x+y)2019的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
①当x>0时,y1>y2; ②当x<0时,x值越大,M值越小;
③使得M大于2的x值不存在; ④使得M=1的x值是![]() 或
或![]() .
.
其中正确的是( )

A.①② B.①④ C.②③ D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线l:y=﹣![]() x+6交y轴于点A,与x轴交于点B,过A、B两点的抛物线m与x轴的另一个交点为C,(C在B的左边),如果BC=5,求抛物线m的解析式,并根据函数图像指出当m的函数值大于0的函数值时x的取值范围.
x+6交y轴于点A,与x轴交于点B,过A、B两点的抛物线m与x轴的另一个交点为C,(C在B的左边),如果BC=5,求抛物线m的解析式,并根据函数图像指出当m的函数值大于0的函数值时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x的一次函数,且当x=-4,y=9;当x=6时,y=-1.
(1)求这个一次函数的解析式和自变量x的取值范围;
(2)当x=-![]() 时,函数y的值;
时,函数y的值;
(3)当y=7时,自变量x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校团委决定对甲、乙、丙三位候选人进行民主投票、笔试、面试考核,从中推选一名担任学生会主席.已知参加民主投票的学生为200名,每人当且仅当推荐一名候选人,民主投票结果如下扇形统计图所示,笔试和面试的成绩如下统计表所示.
甲 | 乙 | 丙 | |
笔试 | 78 | 80 | 85 |
面试 | 92 | 75 | 70 |
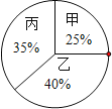
(1)甲、乙、丙的得票数依次是______、______、______;
(2)若民主投票得一票记1分,学校将民主投票、笔试、面试三项得分按3:4:3的比例确定三名候选人的考核成绩,成绩最高当选,请通过计算确定谁当选.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com