
【题目】问题情境:
在平面直角坐标系![]() 中有不重合的两点
中有不重合的两点![]() 和点
和点![]() ,小明在学习中发现,若
,小明在学习中发现,若![]() ,则
,则![]() 轴,且线段
轴,且线段![]() 的长度为
的长度为![]() ;若
;若![]() ,则
,则![]() 轴,且线段
轴,且线段![]() 的长度为
的长度为![]() ;
;
(应用):
(1)若点![]() 、
、![]() ,则
,则![]() 轴,
轴,![]() 的长度为__________.
的长度为__________.
(2)若点![]() ,且
,且![]() 轴,且
轴,且![]() ,则点
,则点![]() 的坐标为__________.
的坐标为__________.
(拓展):
我们规定:平面直角坐标系中任意不重合的两点![]() ,
,![]() 之间的折线距离为
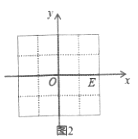
之间的折线距离为![]() ;例如:图1中,点
;例如:图1中,点![]() 与点
与点![]() 之间的折线距离为
之间的折线距离为![]() .
.
解决下列问题:
(1)如图1,已知![]() ,若
,若![]() ,则
,则![]() __________;
__________;
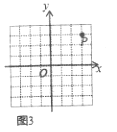
(2)如图2,已知![]() ,
,![]() ,若
,若![]() ,则
,则![]() __________.
__________.
(3)如图3,已知![]() 的,点
的,点![]() 在
在![]() 轴上,且三角形
轴上,且三角形![]() 的面积为3,则
的面积为3,则![]() __________.
__________.

【答案】【应用】:(1)3;(2)(1,2)或(1,2);【拓展】:(1)=5;(2)2或2;(3)4或8
【解析】
(1)根据若y1=y2,则AB∥x轴,且线段AB的长度为|x1x2|,代入数据即可得出结论;
(2)由CD∥y轴,可设点D的坐标为(1,m),根据CD=2即可得出|0m|=2,解之即可得出结论;
(1)根据两点之间的折线距离公式,代入数据即可得出结论;
(2)根据两点之间的折线距离公式结合d(E,H)=3,即可得出关于t的含绝对值符号的一元一次方程,解之即可得出结论;
(3)由点Q在x轴上,可设点Q的坐标为(x,0),根据三角形的面积公式结合三角形OPQ的面积为3即可求出x的值,再利用两点之间的折线距离公式即可得出结论.
解:【应用】:
(1)AB的长度为|12|=3.
故答案为:3.
(2)由CD∥y轴,可设点D的坐标为(1,m),
∵CD=2,
∴|0m|=2,解得:m=±2,
∴点D的坐标为(1,2)或(1,2).
故答案为:(1,2)或(1,2).
【拓展】:
(1)d(E,F)=|2(1)|+|0(2)|=5.
故答案为:=5.
(2)∵E(2,0),H(1,t),d(E,H)=3,
∴|21|+|0t|=3,解得:t=±2.
故答案为:2或2.
(3)由点Q在x轴上,可设点Q的坐标为(x,0),
∵三角形OPQ的面积为3,
∴![]() ,解得:x=±2.
,解得:x=±2.
当点Q的坐标为(2,0)时,d(P,Q)=|32|+|30|=4;
当点Q的坐标为(2,0)时,d(P,Q)=|3(2)|+|30|=8.
故答案为:4或8.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】某风景区集体门票的收费标准是:20人以内(含20人),每人25元;超过20人,超过的部分,每人10元.
(1)写出应收门票费y(元)与游览人数x(人)之间的函数解析式;
(2)利用(1)中的函数解析式计算,某班54名学生要去该风景区游览,购买门票一共需要花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形,点
是等边三角形,点![]() 是直线
是直线![]() 上一点,以
上一点,以![]() 为一边在
为一边在![]() 的右侧作等边
的右侧作等边![]() .
.
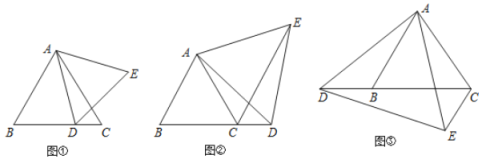
(1)如图①,点![]() 在线段
在线段![]() 上移动时,直接写出
上移动时,直接写出![]() 和
和![]() 的大小关系;
的大小关系;
(2)如图②,点![]() 在线段
在线段![]() 的延长线上移动时,猜想
的延长线上移动时,猜想![]() 的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.
的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 于E,
于E,![]() ,D是AE上的一点,且
,D是AE上的一点,且![]() ,连接BD,CD.
,连接BD,CD.

![]() 试判断BD与AC的位置关系和数量关系,并说明理由;
试判断BD与AC的位置关系和数量关系,并说明理由;
![]() 如图2,若将
如图2,若将![]() 绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
![]() 如图3,若将
如图3,若将![]() 中的等腰直角三角形都换成等边三角形,其他条件不变.
中的等腰直角三角形都换成等边三角形,其他条件不变.
![]() 试猜想BD与AC的数量关系,请直接写出结论;
试猜想BD与AC的数量关系,请直接写出结论;
![]() 你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
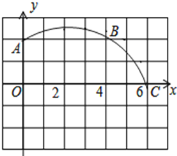
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点
A(0,2),B(4,2)C(6,0),解答下列问题:
(1)请在图中确定该圆弧所在圆心D点的位置,则D点坐标为___ ___;
(2)连结AD,CD,求⊙D的半径(结果保留根号);
(3)若把扇形DAC围成一个圆锥,求围成圆锥的底面半径(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两种型号的机器加工同一种零件,已知A型机器比B型机器每小时多加工20个零件,A型机器加工400个零件所用时间与B型机器加工300个零件所用时间相同.A型机器每小时加工零件的个数_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】猜想与证明:
观察下列各个等式的规律:
第一个等式:![]()
第二个等式:![]()
第三个等式:![]()
第四个等式:![]()
![]()
请用上述等式反映出的规律猜想并证明:
(1)直接写出第五个等式;
(2)问题解决:猜想第 n 个等式(n≥1,用 n 的代数式表示),并证明你猜想的等式是正确的
(3)一个容器装有11水,按照如下要求把水倒出:第1次倒出![]()
![]() 水,第2次倒出的水量是
水,第2次倒出的水量是![]() L水的
L水的![]() ,第3次倒出的水量是
,第3次倒出的水量是![]()
![]() 水的
水的![]() ,第4次倒出的水量是
,第4次倒出的水量是![]()
![]() 水的
水的![]() ,……第
,……第![]() 次倒出的水量是
次倒出的水量是![]() L水的
L水的![]() ,…按照这种倒水的方法,求倒n次水倒出的总水量.
,…按照这种倒水的方法,求倒n次水倒出的总水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC交O于点D,E是弧CD的中点,连接AE交BC于点F,∠ABC=2∠EAC.
(1)求证:AB是⊙O的切线;
(2)若 tanB=![]() ,BD=6,求CF的长.
,BD=6,求CF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是________步.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com