
【题目】猜想与证明:
观察下列各个等式的规律:
第一个等式:![]()
第二个等式:![]()
第三个等式:![]()
第四个等式:![]()
![]()
请用上述等式反映出的规律猜想并证明:
(1)直接写出第五个等式;
(2)问题解决:猜想第 n 个等式(n≥1,用 n 的代数式表示),并证明你猜想的等式是正确的
(3)一个容器装有11水,按照如下要求把水倒出:第1次倒出![]()
![]() 水,第2次倒出的水量是
水,第2次倒出的水量是![]() L水的
L水的![]() ,第3次倒出的水量是
,第3次倒出的水量是![]()
![]() 水的
水的![]() ,第4次倒出的水量是
,第4次倒出的水量是![]()
![]() 水的
水的![]() ,……第
,……第![]() 次倒出的水量是
次倒出的水量是![]() L水的
L水的![]() ,…按照这种倒水的方法,求倒n次水倒出的总水量.
,…按照这种倒水的方法,求倒n次水倒出的总水量.
 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=120,AD⊥BC,且AD=AB.
(1)如图1,DE⊥AB,DF⊥AC,垂足分别为点E,F,求证:AE+AF=AD
(2)如图2,如果∠EDF=60,且∠EDF两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
在平面直角坐标系![]() 中有不重合的两点
中有不重合的两点![]() 和点
和点![]() ,小明在学习中发现,若
,小明在学习中发现,若![]() ,则
,则![]() 轴,且线段
轴,且线段![]() 的长度为
的长度为![]() ;若
;若![]() ,则
,则![]() 轴,且线段
轴,且线段![]() 的长度为
的长度为![]() ;
;
(应用):
(1)若点![]() 、
、![]() ,则
,则![]() 轴,
轴,![]() 的长度为__________.
的长度为__________.
(2)若点![]() ,且
,且![]() 轴,且
轴,且![]() ,则点
,则点![]() 的坐标为__________.
的坐标为__________.
(拓展):
我们规定:平面直角坐标系中任意不重合的两点![]() ,
,![]() 之间的折线距离为
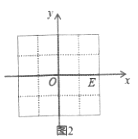
之间的折线距离为![]() ;例如:图1中,点
;例如:图1中,点![]() 与点
与点![]() 之间的折线距离为
之间的折线距离为![]() .
.
解决下列问题:
(1)如图1,已知![]() ,若
,若![]() ,则
,则![]() __________;
__________;
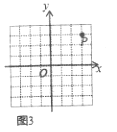
(2)如图2,已知![]() ,
,![]() ,若
,若![]() ,则
,则![]() __________.
__________.
(3)如图3,已知![]() 的,点
的,点![]() 在
在![]() 轴上,且三角形
轴上,且三角形![]() 的面积为3,则
的面积为3,则![]() __________.
__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农八师石河子市某中学初三(1)班的学生,在一次数学活动课中,来到市游憩广场,测量坐落在广场中心的王震将军的铜像高度,已知铜像底座的高为3.5m.某小组的实习报告如下.请你计算出铜像的高(结果精确到0.1m)
实习报告2003年9月25日
题目1 | 测量底部可以到达的铜像高 | |||
| ||||
测 得 数 据 | 测量项目 | 第一次 | 第二次 | 平均值 |
BD的长 | 12.3m | 11.7m | ||
测倾器CD的高 | 1.32m | 1.28m | ||
倾斜角 | α=30°56' | α=31°4' | ||
计 算 | ||||
结果 | ||||
查看答案和解析>>
科目:初中数学 来源: 题型:
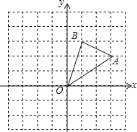
【题目】如图,在边长为![]() 的正方形组成的网格中,
的正方形组成的网格中,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 、
、![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,
,![]() 关于
关于![]() 轴对称的图形为
轴对称的图形为![]() .
.
![]() 画出
画出![]() 并写出点
并写出点![]() 的坐标为________;
的坐标为________;
![]() 写出
写出![]() 的面积为________;
的面积为________;
![]() 点
点![]() 在
在![]() 轴上,使
轴上,使![]() 的值最小,写出点
的值最小,写出点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
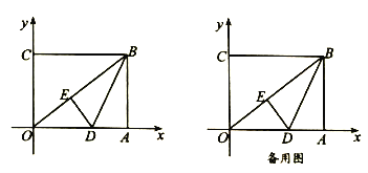
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,矩形
为坐标原点,矩形![]() 的顶点
的顶点![]() 、
、![]() ,将矩形
,将矩形![]() 的一个角
的一个角![]() 沿直线
沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕与
处,折痕与![]() 轴交于点
轴交于点![]() .
.
(1)线段![]() 的长度为__________;
的长度为__________;
(2)求直线![]() 所对应的函数解析式;
所对应的函数解析式;
(3)若点![]() 在线段
在线段![]() 上,在线段
上,在线段![]() 上是否存在点
上是否存在点![]() ,使四边形
,使四边形![]() 是平行四边形?若存在,请求出点
是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
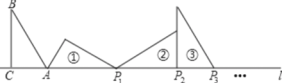
【题目】如图,Rt△ABC中,∠ACB=90°,AC=1,∠B=30°,且AC边在直线l上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时![]() ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时
;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时![]() ;……,按此规律继续旋转,直至得到点
;……,按此规律继续旋转,直至得到点![]() 为止,则
为止,则![]() =___________.
=___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com