
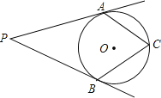
【题目】如图,![]() 、
、![]() 是
是![]() 的切线,切点分别为
的切线,切点分别为![]() 、
、![]() 两点,点
两点,点![]() 在
在![]() 上,如果
上,如果![]() ,那么
,那么![]() 的度数是________.
的度数是________.
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】一轮船在![]() 处测得灯塔
处测得灯塔![]() 在正北方向,灯塔
在正北方向,灯塔![]() 在南偏东
在南偏东![]() 方向,轮船向正东航行了
方向,轮船向正东航行了![]() ,到达
,到达![]() 处,测得
处,测得![]() 位于北偏西
位于北偏西![]() 方向,
方向,![]() 位于南偏西
位于南偏西![]() 方向.
方向.
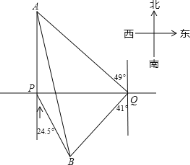
(1)线段![]() 与
与![]() 是否相等?请说明理由;
是否相等?请说明理由;
(2)求![]() 、
、![]() 间的距离(参考数据
间的距离(参考数据![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c (a≠0)的图象如图所示,对称轴是x=-1.下列结论:①ab>0;②b2>4ac;③a-b+2c<0;④8a+c<0.其中正确的是( )

A. ③④ B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某风景区集体门票的收费标准是:20人以内(含20人),每人25元;超过20人,超过的部分,每人10元.
(1)写出应收门票费y(元)与游览人数x(人)之间的函数解析式;
(2)利用(1)中的函数解析式计算,某班54名学生要去该风景区游览,购买门票一共需要花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,DC⊥BC,E是BC上一点,使得AE⊥DE;
(1)求证:△ABE∽△ECD;
(2)若AB=4,AE=BC=5,求CD的长;
(3)当△AED∽△ECD时,请写出线段AD、AB、CD之间数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2, 求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
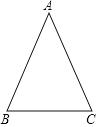
【题目】如图,△ABC是等腰三角形,AB=AC,∠A=36°.
(1)用尺规作∠ABC的角平分线BD,交AC于点D;(保留作图痕迹,不写作法);
(2)过点C作CE//BD,且CE=BD,求证:四边形BCED是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形,点
是等边三角形,点![]() 是直线
是直线![]() 上一点,以
上一点,以![]() 为一边在
为一边在![]() 的右侧作等边
的右侧作等边![]() .
.
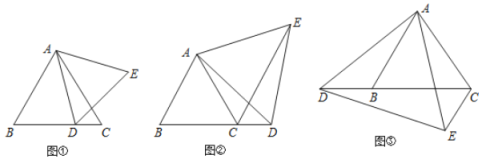
(1)如图①,点![]() 在线段
在线段![]() 上移动时,直接写出
上移动时,直接写出![]() 和
和![]() 的大小关系;
的大小关系;
(2)如图②,点![]() 在线段
在线段![]() 的延长线上移动时,猜想
的延长线上移动时,猜想![]() 的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.
的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】猜想与证明:
观察下列各个等式的规律:
第一个等式:![]()
第二个等式:![]()
第三个等式:![]()
第四个等式:![]()
![]()
请用上述等式反映出的规律猜想并证明:
(1)直接写出第五个等式;
(2)问题解决:猜想第 n 个等式(n≥1,用 n 的代数式表示),并证明你猜想的等式是正确的
(3)一个容器装有11水,按照如下要求把水倒出:第1次倒出![]()
![]() 水,第2次倒出的水量是
水,第2次倒出的水量是![]() L水的
L水的![]() ,第3次倒出的水量是
,第3次倒出的水量是![]()
![]() 水的
水的![]() ,第4次倒出的水量是
,第4次倒出的水量是![]()
![]() 水的
水的![]() ,……第
,……第![]() 次倒出的水量是
次倒出的水量是![]() L水的
L水的![]() ,…按照这种倒水的方法,求倒n次水倒出的总水量.
,…按照这种倒水的方法,求倒n次水倒出的总水量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com