
【题目】如图,△ABC是等腰三角形,AB=AC,∠A=36°.
(1)用尺规作∠ABC的角平分线BD,交AC于点D;(保留作图痕迹,不写作法);
(2)过点C作CE//BD,且CE=BD,求证:四边形BCED是菱形.
【答案】(1)答案见解析;(2)答案见解析
【解析】
(1)利用基本作图作∠ABC的平分线BD;
(2)先利用等腰三角形的性质和三角形内角和计算出∠ABC=∠BCA=![]() (180°﹣∠A)=72°,再利用角平分线定义得到∠CBD=∠ABD=36°,接着根据三角形外角性质得到∠BDC=72°,然后根据等腰三角形的判定定理得到BD=BC,再由四边形DBCE是平行四边形,即可得出结论.
(180°﹣∠A)=72°,再利用角平分线定义得到∠CBD=∠ABD=36°,接着根据三角形外角性质得到∠BDC=72°,然后根据等腰三角形的判定定理得到BD=BC,再由四边形DBCE是平行四边形,即可得出结论.
(1)如图,BD为所作;
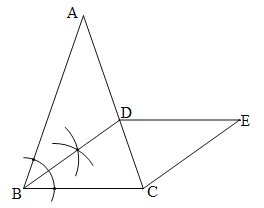
(2)∵AB=AC,∴∠ABC=∠BCA =![]() (180°﹣∠A)=
(180°﹣∠A)=![]() (180°﹣36°)=72°.
(180°﹣36°)=72°.
∵BD平分∠ABC,∴∠CBD=∠ABD=![]() ∠ABC=36°,∴∠BDC=∠A+∠ABD=36°+36°=72°,∴∠BCA =∠BDC,∴BD=BC.
∠ABC=36°,∴∠BDC=∠A+∠ABD=36°+36°=72°,∴∠BCA =∠BDC,∴BD=BC.
∵CE∥BD,CE=BD,∴四边形DBCE是平行四边形,∴平行四边形DBCE是菱形.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
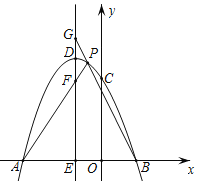
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A、B两点(A在B的左侧),且OA=3,OB=1,与y轴交于C(0,3),抛物线的顶点坐标为D(﹣1,4).
(1)求A、B两点的坐标;
(2)求抛物线的解析式;
(3)过点D作直线DE∥y轴,交x轴于点E,点P是抛物线上B、D两点间的一个动点(点P不与B、D两点重合),PA、PB与直线DE分别交于点F、G,当点P运动时,EF+EG是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在课外学习时遇到这样一个问题:
定义:如果二次函数![]() 与
与![]() 满足
满足![]() ,
,![]() ,
,![]() ,则称这两个函数互为“旋转函数”.
,则称这两个函数互为“旋转函数”.
求函数![]() 的“旋转函数”.
的“旋转函数”.
小明是这样思考的:由函数![]() 可知,
可知,![]() ,
,![]() ,
,![]() ,根据
,根据![]() ,
,![]() ,
,![]() ,求出
,求出![]() ,
,![]() ,
,![]() ,就能确定这个函数的“旋转函数”.
,就能确定这个函数的“旋转函数”.
请参考小明的方法解决下面问题:
(1)直接写出函数![]() 的“旋转函数”;
的“旋转函数”;
(2)若函数![]() 与
与![]() 互为“旋转函数”,求
互为“旋转函数”,求![]() 的值;
的值;
(3)已知函数![]() 的图象与
的图象与![]() 轴交于点A、B两点(A在B的左边),与
轴交于点A、B两点(A在B的左边),与![]() 轴交于点C,点A、B、C关于原点的对称点分别是A1,B1,C1,试证明经过点A1,B1,C1的二次函数与函数
轴交于点C,点A、B、C关于原点的对称点分别是A1,B1,C1,试证明经过点A1,B1,C1的二次函数与函数![]() 互为“旋转函数”。
互为“旋转函数”。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在五张正面分别写有数字﹣2,﹣1,0,1,2的卡片,它们的背面完全相同,现将这五张卡片背面朝上洗匀.
(1)从中任意抽取一张卡片,则所抽卡片上数字的绝对值不大于1的概率是 ;
(2)先从中任意抽取一张卡片,以其正面数字作为a的值,然后再从剩余的卡片随机抽一张,以其正面的数字作为b的值,请用列表法或画树状图法,求点Q(a,b)在第二象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
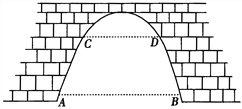
【题目】如图,有一座抛物线型拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m, 就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到桥拱顶.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=120,AD⊥BC,且AD=AB.
(1)如图1,DE⊥AB,DF⊥AC,垂足分别为点E,F,求证:AE+AF=AD
(2)如图2,如果∠EDF=60,且∠EDF两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com