练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某风景区集体门票的收费标准是：20人以内（含20人），每人25元；超过20人，超过的部分，每人10元．

    （1）写出应收门票费y（元）与游览人数x（人）之间的函数解析式；

    （2）利用（1）中的函数解析式计算，某班54名学生要去该风景区游览，购买门票一共需要花多少钱？

    【答案】（1） y=；（2）840元．

    【解析】

    （1）根据题意分别从当0≤x≤20时与当x＞20时求解析式即可；
    （2）当x=54时，x＞20，所以代入第二个解析式求得y的值即是所求．

    解：（1）当0≤x≤20时，y=25x；
    当x＞20时，y=10（x-20）+20×25=10x+300 （其中x是整数），
    综上所述，门票费y（元）与游览人数x（人）之间的关系式为：y=；
    （2）当x=54时，y=10x+300=840（元）．
    答：为购门票共花了840元．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某商人将进货单价为元的某种商品按元销售时，每天可卖出件．现在他采用提高售价的办法增加利润，已知这种商品销售单价每涨元，销售量就减少件，那么他将售价每个定为________元时，才能使每天所赚的利润最大，每天最大利润是________元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

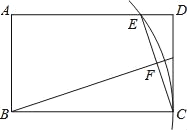
    【题目】如图，在矩形ABCD中，AB=3，BC=5，以B为圆心BC为半径画弧交AD于点E，连接CE，作BF⊥CE，垂足为F，则tan∠FBC的值为（　　）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，反比例函数y= 的图象与一次函数y=x+b的图象交

    于点A（1，4）、点B（-4，n）．

    （1）求一次函数和反比例函数的解析式；

    （2）求△OAB的面积；

    （3）直接写出一次函数值大于反比例函数值的自变量x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

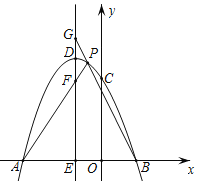
    【题目】如图，在平面直角坐标系中，抛物线y=ax2+bx+c交x轴于A、B两点（A在B的左侧），且OA=3，OB=1，与y轴交于C（0，3），抛物线的顶点坐标为D（﹣1，4）．

    （1）求A、B两点的坐标；

    （2）求抛物线的解析式；

    （3）过点D作直线DE∥y轴，交x轴于点E，点P是抛物线上B、D两点间的一个动点（点P不与B、D两点重合），PA、PB与直线DE分别交于点F、G，当点P运动时，EF+EG是否为定值？若是，试求出该定值；若不是，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在“爱我永州”中学生演讲比赛中，五位评委分别给甲、乙两位选手的评分如下：

    甲：8、7、9、8、8

    乙：7、9、6、9、9

    则下列说法中错误的是（ ）

    A．甲、乙得分的平均数都是8

    B．甲得分的众数是8，乙得分的众数是9

    C．甲得分的中位数是9，乙得分的中位数是6

    D．甲得分的方差比乙得分的方差小

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，、是的切线，切点分别为、两点，点在上，如果，那么的度数是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在五张正面分别写有数字﹣2，﹣1，0，1，2的卡片，它们的背面完全相同，现将这五张卡片背面朝上洗匀．

    （1）从中任意抽取一张卡片，则所抽卡片上数字的绝对值不大于1的概率是 ；

    （2）先从中任意抽取一张卡片，以其正面数字作为a的值，然后再从剩余的卡片随机抽一张，以其正面的数字作为b的值，请用列表法或画树状图法，求点Q（a，b）在第二象限的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题情境：

    在平面直角坐标系中有不重合的两点和点，小明在学习中发现，若，则轴，且线段的长度为；若，则轴，且线段的长度为；

    （应用）：

    （1）若点、，则轴，的长度为__________．

    （2）若点，且轴，且，则点的坐标为__________．

    （拓展）：

    我们规定：平面直角坐标系中任意不重合的两点，之间的折线距离为；例如：图1中，点与点之间的折线距离为．

    解决下列问题：

    （1）如图1，已知，若，则__________；

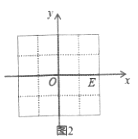
    （2）如图2，已知，，若，则__________．

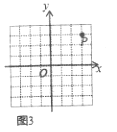
    （3）如图3，已知的，点在轴上，且三角形的面积为3，则__________．

    查看答案和解析>>

    同步练习册答案