
【题目】某商人将进货单价为![]() 元的某种商品按
元的某种商品按![]() 元销售时,每天可卖出
元销售时,每天可卖出![]() 件.现在他采用提高售价的办法增加利润,已知这种商品销售单价每涨
件.现在他采用提高售价的办法增加利润,已知这种商品销售单价每涨![]() 元,销售量就减少
元,销售量就减少![]() 件,那么他将售价每个定为________元时,才能使每天所赚的利润最大,每天最大利润是________元.
件,那么他将售价每个定为________元时,才能使每天所赚的利润最大,每天最大利润是________元.
科目:初中数学 来源: 题型:
【题目】某中学开展“数学史”知识竞赛活动,八年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
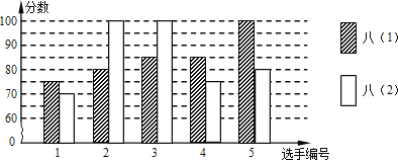
(1)请计算八(1)班、八(2)班两个班选出的5名选手复赛的平均成绩;
(2)请判断哪个班选出的5名选手的复赛成绩比较稳定,并说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=12,点F是AB的中点,过点F作FD⊥AB交AC于点D.
(1)若△AFD以每秒2个单位长度的速度沿射线FB向右移动,得到△A1F1D1,当F1与点B重合时停止移动.设移动时间为t秒,△A1F1D1与△CBF重叠部分的面积记为S.直接写出S与t的函数关系式.
(2)在(1)的基础上,如果D1,B,F构成的△D1BF为等腰三角形,求出t值.
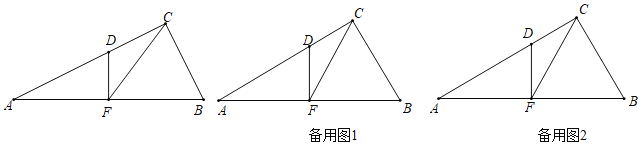
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象的对称轴是直线![]() ,它与
,它与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交与点
轴交与点![]() ,点
,点![]() 、
、![]() 的坐标分别是
的坐标分别是![]() 、
、![]() .
.

(1)请在平面直角坐标系内画出示意图;
(2)求此图象所对应的函数关系式;
(3)若点![]() 是此二次函数图象上位于
是此二次函数图象上位于![]() 轴上方的一个动点,求
轴上方的一个动点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A、B的坐标分别为(-4,0)和(2,0),BC=![]() .设直线AC与直线x=4交于点E.
.设直线AC与直线x=4交于点E.
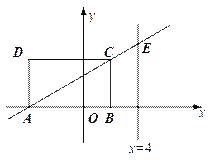
(1)求以直线x=4为对称轴,且过C与原点O的抛物线的函数关系式,并说明此抛物线一定过点E;
(2)设(1)中的抛物线与x轴的另一个交点为N,M是该抛物线上位于C、N之间的一动点,求△CMN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一轮船在![]() 处测得灯塔
处测得灯塔![]() 在正北方向,灯塔
在正北方向,灯塔![]() 在南偏东
在南偏东![]() 方向,轮船向正东航行了
方向,轮船向正东航行了![]() ,到达
,到达![]() 处,测得
处,测得![]() 位于北偏西
位于北偏西![]() 方向,
方向,![]() 位于南偏西
位于南偏西![]() 方向.
方向.
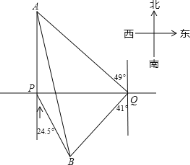
(1)线段![]() 与
与![]() 是否相等?请说明理由;
是否相等?请说明理由;
(2)求![]() 、
、![]() 间的距离(参考数据
间的距离(参考数据![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某风景区集体门票的收费标准是:20人以内(含20人),每人25元;超过20人,超过的部分,每人10元.
(1)写出应收门票费y(元)与游览人数x(人)之间的函数解析式;
(2)利用(1)中的函数解析式计算,某班54名学生要去该风景区游览,购买门票一共需要花多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com