
【题目】如图,△ABC和△ADE均为等腰直角三角形,连接BE,点F、G分别为AD、AC的中点,连接FG.在△ADE绕A旋转的过程中,当B、D、E三点共线时,AB=![]() ,AD=1,则线段FG的长为___.
,AD=1,则线段FG的长为___.

【答案】1
【解析】
连接CD、CE,如图,证明△ABD≌△ACE,可得BD=CE,∠ABD=∠ACE,继而可得∠CED=90°,设CE=x,则BE=x+![]() ,在Rt△BCE中,利用勾股定理可求得CE的长,在Rt△CDE中,利用勾股定理可求得CD长,然后再利用三角形中位线定理即可求得FG长.
,在Rt△BCE中,利用勾股定理可求得CE的长,在Rt△CDE中,利用勾股定理可求得CD长,然后再利用三角形中位线定理即可求得FG长.
连接CD、CE,如图,
∵△ABC和△ADE均为等腰直角三角形,
∴AB=AC,BC=![]() AB=
AB=![]() ,AD=AE,DE=
,AD=AE,DE=![]() AD=
AD=![]() ,∠BAC=∠DAE=90°,∠ADE=∠AED=45°,
,∠BAC=∠DAE=90°,∠ADE=∠AED=45°,
∴∠BAD=∠CAE,
在△ABD和△ACE中
 ,
,
∴△ABD≌△ACE,
∴BD=CE,∠ABD=∠ACE,
∵∠ADE=∠ABD+∠BAD=45°,
∴∠CAE+∠ACE=45°,
∴∠CED=90°,
设CE=x,则BE=x+![]() ,
,
在Rt△BCE中,x2+(x+![]() )2=(
)2=(![]() )2,
)2,
解得x1=﹣2![]() ,x2=
,x2=![]() ,
,
∴CE=![]() ,
,
在Rt△CDE中,CD=![]() =2,
=2,
∵点F、G分别为AD、AC的中点,
∴FG为△ADC的中位线,
∴FG=![]() CD=1,
CD=1,
故答案为:1.


科目:初中数学 来源: 题型:
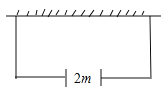
【题目】如图,若要建一个长方形鸡场,鸡场的一边靠墙,墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,围成长方形的鸡场除门之外四周不能有空隙.求:
(1)若墙长为18米,要围成鸡场的面积为150平方米,则鸡场的长和宽各为多少米?
(2)围成鸡场的面积可能达到200平方米吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在等腰△ABC中,AB=AC=![]() ,BC=4,点D从A出发以每秒
,BC=4,点D从A出发以每秒![]() 个单位的速度向点B运动,同时点E从点B出发以每秒4个单位的速度向点C运动,在DE的右侧作∠DEF=∠B,交直线AC于点F,设运动的时间为t秒,则当△ADF是一个以AD为腰的等腰三角形时,t的值为_____.
个单位的速度向点B运动,同时点E从点B出发以每秒4个单位的速度向点C运动,在DE的右侧作∠DEF=∠B,交直线AC于点F,设运动的时间为t秒,则当△ADF是一个以AD为腰的等腰三角形时,t的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C三点在同一直线上,分别以AB、BC为边,在直线AC的同侧作等边△ABD和等边△BCE,连接AE交BD于点M,连接CD交BE于点N,连接MN得△BMN.

(1)求证:AE=CD;
(2)试判断△BMN的形状,并说明理由;
(3)设CD、AE相交于点G,求∠AGC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道“对称补缺”的思想是解决与轴对称图形有关的问题的一种重要的添加辅助线的策略,参考这种思想解决下列问题.
在△ABC中,D为△ABC外一点.

(1)如图1,若AC平分∠BAD,CE⊥AB于点E,∠ B+∠ADC=180,求证:BC=CD;
(2)如图2,若∠ACB=90°, AC=BC,F是AC上一点,AD⊥BF交BF延长线于点D,且BF是∠CBA的角平分线.求证:2AD=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D.

(1)求直线BC的解析式;
(2)如图2,点P为直线BC上方抛物线上一点,连接PB、PC.当△PBC的面积最大时,在线段BC上找一点E(不与B、C重合),使PE+![]() BE的值最小,求点P的坐标和PE+
BE的值最小,求点P的坐标和PE+![]() BE的最小值;
BE的最小值;
(3)如图3,点G是线段CB的中点,将抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() .
.
⑴已知线段AB的垂直平分线与BC边交于点P,连结AP,求证:![]() ;
;
⑵以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连结AQ,若![]() ,求
,求![]() 的度数.
的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲乙两名采购员去同一家饲料公司分别购买两次饲料,两次购买饲料价格分别为m元/千克和n元/千克,且m≠n,两名采购员的采购方式也不同,其中甲每次购买1000千克,乙每次用去800元,而不管购买多少饲料.
(1)甲、乙所购饲料的平均单价各是多少?(用字母m、n表示)
(2)谁的购货方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:已知∠MAB=60°,以AB的长为菱形ABCD的边长,点D在AM上,
(1)作出这个菱形.(保留作图痕迹,不写作法,不用证明)
(2)若AB=2,则对角线AC的长为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com