
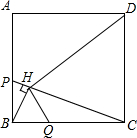
 如图,在正方形ABCD中,P为AB上一点,过B点作PC的垂线,垂足H,过H作HQ⊥DH交BC于Q.求证:BP=BQ.
如图,在正方形ABCD中,P为AB上一点,过B点作PC的垂线,垂足H,过H作HQ⊥DH交BC于Q.求证:BP=BQ. 分析 首先得出△HBQ∽△HCD,可得出$\frac{BQ}{BH}$=$\frac{CD}{HC}$,而在Rt△BCP,通过相似三角形△BPH和△CPH,可得出$\frac{BP}{BH}$=$\frac{BC}{HC}$,联立两个比例关系式,即可得出所证的结论.
解答 证明:∵BH⊥PC,
∴∠HBC+∠HCB=90°,
又∵∠HCB+∠HCD=90°,
∴∠HBC=∠HCD,
∵HD⊥HQ,
∴∠DHQ=90°,
∵∠BHC=∠BHQ+∠CHQ=90°,∠DHQ=∠DHC+∠CHQ=90°,
∴∠BHQ=∠DHC,
∴△HBQ∽△HCD(两角对应相等的两个三角形相似),
∴$\frac{BQ}{BH}$=$\frac{CD}{HC}$,
又∵BH⊥PC,
∴△HBP∽△HCB,
∴$\frac{BP}{BH}$=$\frac{BC}{HC}$,
∵BC=CD,
∴$\frac{BQ}{BH}$=$\frac{BP}{BH}$,
∴BQ=BP.
点评 本题考查了相似三角形的判定与性质及正方形的性质,难度适中,关键是掌握相似三角形的判定方法.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 了解全班同学每周体育锻炼的时间 | B. | 了解全市中小学生每天的零花钱 | ||
| C. | 学校招聘教师,对应聘人员面试 | D. | 旅客上飞机前的安检 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,7) | B. | (6,3) | C. | (-2,3) | D. | (2,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com