
分析 ①求出b2-4ac的值,再代入公式求出即可.
②方程移项后利用因式分解法求出解即可.
解答 解:①3x2+x-1=0
a=3,b=1,c=-1,
△=b2-4ac=1+12=13>0,
x=$\frac{-1±\sqrt{13}}{2×3}$,
∴x1=$\frac{-1+\sqrt{13}}{6}$,x2=$\frac{-1-\sqrt{13}}{6}$.
②(3x-2)2=4(3-x)2,
移项得:(3x-2)2-4(3-x)2,=0,
分解因式得:[(3x-2)+2(3-x)][(3x-2)-2(3-x)]=0,
可得x+4=0或5x-8=0,
解得:x1=-4,x2=$\frac{8}{5}$.
点评 本题考查了解一元二次方程的应用,能选择适当的方法解一元二次方程是解此题的关键,此题是一道中档题目,难度适中.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
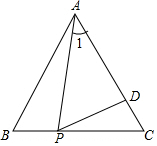 如图,在等边△ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=$\frac{2}{3}$.
如图,在等边△ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD=$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com