

·ضخِ £¨1£©بçح¼1£¬ء¬½سAC£¬¸ù¾فءâذخµؤذشضتض¤أ÷،÷ABC؛ح،÷ACDتاµب±كب½اذخ£¬µأ،دB=،دACQ£¬AB=AC£¬¸ù¾فء½¶¯µمشث¶¯µؤثظ¶بدàµب؟ةضھ£؛BP=CQ=t£¬ض¤أ÷،÷ABP،ص،÷ACQ£¬µأAP=AQ¼°،دPAQ=60،م£¬ثùزش،÷APQخھµب±كب½اذخ£»
£¨2£©بçح¼2£¬رس³¤QP½»ABµؤرس³¤دكسعµمM£¬دب¸ù¾فت±¼نخھ1¼ئثمBP؛حCPµؤ³¤£¬شظ¸ù¾فAM،خCD£¬ءذ±بہت½£؛$\frac{BM}{CQ}=\frac{BP}{PC}$؛ح$\frac{AK}{KC}=\frac{AM}{CQ}$£¬دباَBMµؤ³¤£¬شظاَAK£»
£¨3£©×÷¸¨ضْدك£¬¹¹½¨¸كدك£¬ةèBE=x£¬دبض¤أ÷،÷BEP،×،÷CPF£¬اَFC،¢BE،¢AE؛حAFµؤ³¤£¬¸ù¾فجطتâ½اµؤب½ا؛¯تضµاَ¸كدكGF،¢EHµؤ³¤£¬ض¤أ÷PQسëFC´¹ض±£¬ہûسأأو»²îاَS،÷EPFµؤأو»£®
½â´ً ½â£؛£¨1£©،÷APQخھµب±كب½اذخ£¬ہيسةتا£؛
بçح¼1£¬ء¬½سAC£¬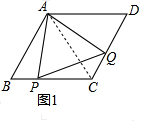
،كثؤ±كذخABCDخھءâذخ£¬
،àAB=BC£¬
،ك،دB=60،م£¬
،à،÷ABCتاµب±كب½اذخ£¬
ح¬ہي؟ةµأ£؛،÷ACDتاµب±كب½اذخ£¬
،à،دB=،دACQ=60،م£¬
،كAB=AC£¬BP=CQ=t£¬
،à،÷ABP،ص،÷ACQ£¬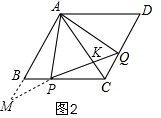
،àAP=AQ£¬،دBAP=،دCAQ£¬
،ك،دBAP+،دPAC=60،م£¬
،à،دCAQ+،دPAC=60،م£¬
¼´،دPAQ=60،م£¬
،à،÷APQخھµب±كب½اذخ£»
£¨2£©بçح¼2£¬µ±t=1ت±£¬BP=CQ=1£¬CP=3£¬
رس³¤QP½»ABµؤرس³¤دكسعµمM£¬
،كAM،خCD£¬
،à$\frac{BM}{CQ}=\frac{BP}{PC}$£¬
،à$\frac{BM}{1}=\frac{1}{3}$£¬
،àBM=$\frac{1}{3}$£¬
،àAM=AB+BM=4+$\frac{1}{3}$=$\frac{13}{3}$£¬
،كAM،خCD£¬
،à$\frac{AK}{KC}=\frac{AM}{CQ}$£¬
،à$\frac{AK}{KC}=\frac{\frac{13}{3}}{1}$=$\frac{13}{3}$£¬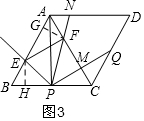
،à$\frac{AK}{AC}=\frac{13}{16}$£¬
،à$\frac{AK}{4}=\frac{13}{16}$£¬
،àAK=$\frac{13}{4}$£¬
شٍAKµؤ³¤تا$\frac{13}{4}$£»
£¨3£©بçح¼3£¬ةèذ×ھ¦ء¶ب£¬شٍ،دNPQ=،دAPE=¦ء£¬
ةèBE=x£¬
µ±t=2ت±£¬BP=PC=2£¬
،كPتاBCµؤضذµم£¬،÷ABCتاµب±كب½اذخ£¬
،àAP،حBC£¬
،à،دAPC=90،م£¬
،à،دFPC=90،م-،دAPN=90،م-£¨60،م-¦ء£©=30،م+¦ء£¬
،ك،دPEB=،دBAP+،دAPE=30،م+¦ء£¬
،à،دPEB=،دFPC£¬
،ك،دB=،دFCP£¬
،à،÷BEP،×،÷CPF£¬
،à$\frac{BE}{PC}=\frac{BP}{CF}$£¬
،à$\frac{x}{2}=\frac{2}{CF}$£¬
،àCF=$\frac{4}{x}$£¬
،كAD،خBC£¬
،à$\frac{AN}{CP}=\frac{AF}{FC}$£¬
،à$\frac{1}{2}=\frac{AF}{FC}$£¬
،à$\frac{1}{3}=\frac{AF}{AC}=\frac{AF}{4}$£¬
،àAF=$\frac{4}{3}$£¬FC=$\frac{8}{3}$£¬
شٍ$\frac{4}{x}=\frac{8}{3}$£¬x=$\frac{3}{2}$£¬
،àBE=$\frac{3}{2}$£¬
،àAE=4-$\frac{3}{2}$=$\frac{5}{2}$£¬
¹F×÷FG،حABسعG£¬¹E×÷EH،حBCسعH£¬
sin60،م=$\frac{FG}{AF}$£¬sin60،م=$\frac{EH}{BE}$£¬
FG=$\frac{\sqrt{3}}{2}$،ء$\frac{4}{3}$=$\frac{2\sqrt{3}}{3}$£¬EH=$\frac{\sqrt{3}}{2}$،ء$\frac{3}{2}$=$\frac{3\sqrt{3}}{4}$£¬
شع،÷PCQضذ£¬،دPCQ=120،م£¬
،كPC=CQ£¬
،à،دQPC=،دPQC=30،م£¬
،ك،دPCM=60،م£¬
،à،دPMC=90،م£¬
،àPM=$\sqrt{3}$£¬
،àS،÷PEF=S،÷ABC-S،÷AEF-S،÷PEB-S،÷PFC£¬
=$\frac{1}{2}$BC•AP-$\frac{1}{2}$AE•GF-$\frac{1}{2}$PB•EH-$\frac{1}{2}$FC•PM£¬
=$\frac{1}{2}$،ء4،ء2$\sqrt{3}$-$\frac{1}{2}$،ء$\frac{5}{2}$،ء$\frac{2\sqrt{3}}{3}$-$\frac{1}{2}،ء2،ء\frac{3\sqrt{3}}{4}$-$\frac{1}{2}$،ء$\frac{8}{3}$،ء$\sqrt{3}$£¬
=$\frac{13\sqrt{3}}{12}$£®
µمئہ ±¾جâتاثؤ±كذخµؤ×غ؛دج⣬؟¼²éءثءâذخ،¢ب«µبب½اذخ،¢µب±كب½اذخµؤذشضت؛حإذ¶¨£»µع£¨1£©ختضذؤـض¤أ÷،÷ABP،ص،÷ACQتاح»ئئ؟ع£»µع£¨2£©ختا،µ±µط×÷¸¨ضْدك£¬¹¹½¨ئ½ذذدك·ضدك¶خ³ة±بہ¶¨ہيتا¹ط¼ü£»µع£¨3£©ہûسأب½اذخدàثئاَ±كµؤ³¤¶ب£¬·ض±ًاَب½اذخµؤ¸كدك£¬´ْبëأو»¹«ت½؟ةµأ½لآغ£®


 إàسإ؟عثمجâ؟¨دµءذ´ً°¸
إàسإ؟عثمجâ؟¨دµءذ´ً°¸ ؟ھذؤ؟عثمجâ؟¨دµءذ´ً°¸
؟ھذؤ؟عثمجâ؟¨دµءذ´ً°¸ ؟عثمجâ؟¨؛س±±ةظؤê¶ùح¯³ِ°وةçدµءذ´ً°¸
؟عثمجâ؟¨؛س±±ةظؤê¶ùح¯³ِ°وةçدµءذ´ً°¸
| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛جî؟صجâ
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛ر،شٌجâ
| A£® |  | B£® | 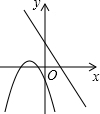 | C£® | 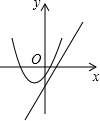 | D£® | 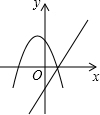 |
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛جî؟صجâ
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛½â´ًجâ

²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛½â´ًجâ
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛ر،شٌجâ
| A£® | a£¾3 | B£® | a£¼3ازa،ظ-1 | C£® | a£¼3 | D£® | a،ف3ازa،ظ-1 |
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛½â´ًجâ
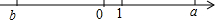 تضلةدسذb£¬0£¬1£¬aµؤثؤ¸ِت£¬بçح¼ثùت¾£¬زرضھ|a|=|b|£¬»¯¼ٍ£؛|b+1|+|$\frac{a}{b}$|-|a+b|£®
تضلةدسذb£¬0£¬1£¬aµؤثؤ¸ِت£¬بçح¼ثùت¾£¬زرضھ|a|=|b|£¬»¯¼ٍ£؛|b+1|+|$\frac{a}{b}$|-|a+b|£®²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛½â´ًجâ
²é؟´´ً°¸؛ح½âخِ>>
¹ْ¼تر§ذ£سإر، - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com