
如图1,菱形ABCD中,∠A=60°,点P从A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止,点Q从A与P同时出发,沿边AD匀速运动到D终止,设点P运动的时间为t(s).△APQ的面积S(cm2)与t(s)之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出.
(1)求点Q运动的速度;
(2)求图2中线段FG的函数关系式;
(3)问:是否存在这样的t,使PQ将菱形ABCD的面积恰好分成1:5的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
(1)点Q运动的速度是1cm/s;(2) ;(3)存在,t=
;(3)存在,t= 或t=
或t= .
.
解析试题分析:(1)根据函数图象中E点所代表的实际意义求解.E点表示点P运动到与点B重合时的情形,运动时间为3s,可得AB=6cm;再由S△APQ= ,可求得AQ的长度,进而得到点Q的运动速度;
,可求得AQ的长度,进而得到点Q的运动速度;
(2)函数图象中线段FG,表示点Q运动至终点D之后停止运动,而点P在线段CD上继续运动的情形.如答图2所示,求出S的表达式,并确定t的取值范围;
(3)当点P在AB上运动时,PQ将菱形ABCD分成△APQ和五边形PBCDQ两部分,如答图3所示,求出t的值;当点P在BC上运动时,PQ将菱形分为梯形ABPQ和梯形PCDQ两部分,如答图4所示,求出t的值.
试题解析:(1)由题意,可知题图2中点E表示点P运动至点B时的情形,所用时间为3s,则菱形的边长AB=2×3=6cm.此时如答图1所示:
AQ边上的高h=AB•sin60°=6× =
= cm, S=S△APQ=
cm, S=S△APQ= AQ•h=
AQ•h= AQ×3
AQ×3 =
= ,解得AQ=3cm.∴点Q的运动速度为:3÷3=1cm/s.(2)由题意,可知题图2中FG段表示点P在线段CD上运动时的情形.如答图2所示:
,解得AQ=3cm.∴点Q的运动速度为:3÷3=1cm/s.(2)由题意,可知题图2中FG段表示点P在线段CD上运动时的情形.如答图2所示:
点Q运动至点D所需时间为:6÷1=6s,点P运动至点C所需时间为12÷2=6s,至终点D所需时间为18÷2=9s.
因此在FG段内,点Q运动至点D停止运动,点P在线段CD上继续运动,且时间t的取值范围为:6≤t≤9.过点P作PE⊥AD交AD的延长线于点E,则PE=PD•sin60°=(18-2t)× ,
,
S=S△APQ= AD•PE=
AD•PE= ×6×(?
×6×(? +
+ )=
)= .
.
∴FG段的函数表达式为:S= (6≤t≤9).
(6≤t≤9).
(3)菱形ABCD的面积为:6×6×sin60°=18 ,
,
当点P在AB上运动时,PQ将菱形ABCD分成△APQ和五边形PBCDQ两部分,如答图3所示.
此时△APQ的面积S= AQ•AP•sin60°=
AQ•AP•sin60°= t•2t×
t•2t× =
= ,
,
根据题意,得 =
= ,
,
解得:t= s,
s,
当点P在BC上运动时,PQ将菱形分为梯形ABPQ和梯形PCDQ两部分,如答图4所示.
此时,有S梯形ABPQ= S菱形ABCD,即
S菱形ABCD,即 (2t-6+t)×6×
(2t-6+t)×6× =
= ×18
×18 ,
,
解得t= s,
s,
答:存在,当t= 或
或 时,使PQ将菱形ABCD的面积恰好分成1:5的两部分.
时,使PQ将菱形ABCD的面积恰好分成1:5的两部分.
考点:1、相似形综合题;2、动点问题的函数图象.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
如图,△ABC在坐标平面内三个顶点的坐标分别为A(1,2)、B(3,3)、C(3,1).
(1)根据题意,请你在图中画出△ABC;
(2)在原图中,以B为位似中心,画出△A′BC′使它与△ABC位似且位似比是3:1,并写出顶点A′和C′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图①,已知线段AB=8,以AB为直径作半圆O,再以OA为直径作半圆C,P是半圆C上的一个动点(P与点A,O不重合),AP的延长线交半圆O于点D。
(1)判断线段AP与PD的大小关系,并说明理由;
(2)连接PC,当∠ACP=600时,求弧AD的长;
(3)过点D作DE⊥AB,垂足为E(如图②),设AP=x,OE=y,求y与x之间的函数关系式,并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.(1)如图1,若四边形ABCD是矩形,且DE⊥CF.则
 (填“<”或“=”或“>”);
(填“<”或“=”或“>”);
(2)如图2,若四边形ABCD是平行四边形,试探究:
当∠B与∠EGC满足什么关系时,使得 =
= 成立?并证明你的结论;
成立?并证明你的结论;
(3)如图3,若BA="BC=" 3,DA="DC=" 4,∠BAD= 90°,DE⊥CF.则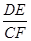 的值为 .
的值为 .
图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知△ABC是边长为6cm的等边三角形,动点P,Q同时从A、B两点出发,分别沿AB,BC方向匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),
解答下列问题:
(1)当 为何值时,△BPQ为直角三角形;
为何值时,△BPQ为直角三角形;
(2)设△BPQ的面积为S(cm2),求S与 的函数关系式;
的函数关系式;
(3)作QR∥BA交AC于点R,连结PR,当 为何值时,△APR∽△PRQ ?
为何值时,△APR∽△PRQ ?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
晚上,小亮走在大街上.他发现:当他站在大街两边的两盏路灯之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子长为3米,左边的影子长为1.5米.又知自己身高1.80米,两盏路灯的高相同,两盏路灯之间的距离为12米.求路灯的高.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,E是BC的中点,连接AE、AC.
求证:(1)点F是DC上一点,连接EF,交AC于点O(如图1),△AOE∽△COF;
(2)若点F是DC的中点,连接BD,交AE与点G(如图2),求证:四边形EFDG是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD,垂足为E.
(1)求证:△ABE∽△DBC;
(2)求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,矩形ABCD中,AB=12cm,AD=16cm,动点E、F分别从A点、C点同时出发,均以2cm/s的速度分别沿AD向D点和沿CB向B点运动。
(1)经过几秒首次可使EF⊥AC?
(2)若EF⊥AC,在线段AC上,是否存在一点P,使 ?若存在,请说明P点的位置,并予以证明;若不存在,请说明理由。
?若存在,请说明P点的位置,并予以证明;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com