
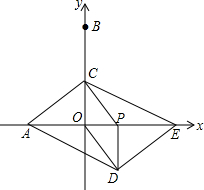
 ��ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ��ǣ�-2��0������0��4��������P��O��������x����������ÿ��1����λ���ٶ��˶���ͬʱ����C��ÿ��2����λ���ٶ���y���ϴӵ�B�����˶�����Oֹͣ����Cֹͣ�˶�ʱ��PҲ��ֹ֮ͣ�˶�����CP��COΪ�ڱ߹���ƽ���ı���PCOD�����߶�OP���ӳ��߳�ȡ��E��ʹ��PE=2�����P���˶�ʱ��Ϊt�룮
��ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ��ǣ�-2��0������0��4��������P��O��������x����������ÿ��1����λ���ٶ��˶���ͬʱ����C��ÿ��2����λ���ٶ���y���ϴӵ�B�����˶�����Oֹͣ����Cֹͣ�˶�ʱ��PҲ��ֹ֮ͣ�˶�����CP��COΪ�ڱ߹���ƽ���ı���PCOD�����߶�OP���ӳ��߳�ȡ��E��ʹ��PE=2�����P���˶�ʱ��Ϊt�룮���� ��1��������CD��OP�ڵ�G����?PCOD�ĶԽ�����ƽ�֣����ı���ADEC��ƽ���ı��Σ�
����?PCOD�ĶԽ�����ȣ���ƽ���ı���ADECΪ���Σ�
��2���ٵ�һ�����������M��CE����ʱ���ɡ�EMF�ס�ECO�������������ζԽ��������⣻�ڶ������������N��DE����ʱ���ɡ�EFN�ס�EPD�������������ζԽ��������⣻
�ڵ�$\frac{2}{3}$��t��1ʱ�����S��ȡֵ��Χ��
��� ��1����֤��������CD��OP�ڵ�G��
��?PCOD��CG=DG��OG=PG��
��AO=2��PE=2��
��AO=PE��
��AG=EG��
���ı���ADEC��ƽ���ı��Σ�
�ڽ⣺��AE=CDʱ��ƽ���ı���ADECΪ���Σ�
��AO=2��OP=t��PE=2����AE=4+t��
�֡�BC=2t��
��OC=4-2t��
��OG=$\frac{1}{2}t$��
��CG2=��4-2t��2+��$\frac{1}{2}$t��2��
��CD2=4[��4-2t��2+��$\frac{1}{2}$t��2]��
AE2=��4+t��2��
ƽ���ı���ADECΪ���Σ���4+t��2=4[��4-2t��2+��$\frac{1}{2}$t��2]��
��ã�t=$\frac{9+\sqrt{33}}{4}$��t=$\frac{9-\sqrt{33}}{4}$��
��OB=4��
��0��t��2��
��t=$\frac{9-\sqrt{33}}{4}$��
��2���⣺�ٵ�M����CE��ʱ����һ���������ͼ������M��CE����ʱ��
��MF��OC��
���EMF�ס�ECO��
��$\frac{MF}{CO}=\frac{EF}{EO}$��
���ı���MPNEΪ�����Σ�
��MF=EF��
��CO=EO����4-2t=t+2��
��t=$\frac{2}{3}$��
�ڶ������������N��DE��ʱ��
��NF��PD��
���EFN�ס�EPD��
��$\frac{FN}{PD}$=$\frac{FE}{PE}$��
���ı���MPNEΪ�����Σ�
��NF=EF��
��PD=PE����4-2t=2��
��t=1��
�൱��M��N����һ�������ı���ADEC�ı���ʱ����������������t��ֵΪt=$\frac{2}{3}$��t=1��
�ڽ⣺��$\frac{2}{3}$��t��1��
S=��4-2t��t=-2t2+4t=-2��t-1��2+2��
���M��N��ǡ��ֻ��һ�������ı���ADEC���ڲ����������߽磩ʱ��
$\frac{16}{9}��S��2$��
���� ������Ҫ������ƽ���ı��ε��ж����������ε��ж������������ε��ж��������ۺ������ı��ε��ж������ʣ��������ۣ����ν���ǽ�����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | M��-2��3�� | B�� | M��-2��-3�� | C�� | M��2��3�� | D�� | M��2��-3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 5$\sqrt{5}$ | C�� | 8 | D�� | 10$\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com