
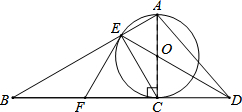
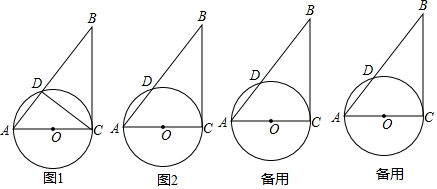
 已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.分析 (1)连接FO,由F为BC的中点,AO=CO,得到OF∥AB,由于AC是⊙O的直径,得出CE⊥AE,根据OF∥AB,得出OF⊥CE,于是得到OF所在直线垂直平分CE,推出FC=FE,OE=OC,再由∠ACB=90°,即可得到结论.
(2)证出△AOE是等边三角形,得到∠EOA=60°,再由直角三角形的性质即可得到结果.
(3)如图3中,作AG⊥DE于G.由AG2=OA2-OG2=AE2-EG2,求出OG、AG,再利用△AGO∽△DCO,得$\frac{CD}{AG}$=$\frac{OC}{OG}$,求出CD即可.
解答 证明:(1)如图1,连接FO,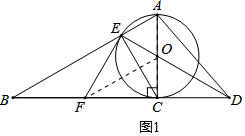
∵F为BC的中点,AO=CO,
∴OF∥AB,
∵AC是⊙O的直径,
∴CE⊥AE,
∵OF∥AB,
∴OF⊥CE,
∴OF所在直线垂直平分CE,
∴FC=FE,OE=OC,
∴∠FEC=∠FCE,∠0EC=∠0CE,
∵∠ACB=90°,
即:∠0CE+∠FCE=90°,
∴∠0EC+∠FEC=90°,
即:∠FEO=90°,
∴FE为⊙O的切线;
(2)如图2,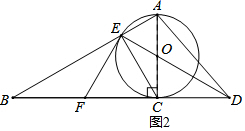
∵⊙O的半径为3,
∴AO=CO=EO=3,
∵∠EAC=60°,OA=OE,
∴∠EOA=60°,
∴∠COD=∠EOA=60°,
∵在Rt△OCD中,∠COD=60°,OC=3,
∴CD=3$\sqrt{3}$,
∵在Rt△ACD中,∠ACD=90°,
CD=3$\sqrt{3}$,AC=6,
∴AD=3$\sqrt{7}$.
(3)如图3中,作AG⊥DE于G.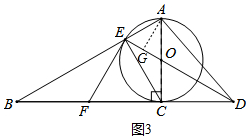
∵AG2=OA2-OG2=AE2-EG2,
∴r2-OG2=22-(r-OG)2,
∴OG=$\frac{{r}^{2}-2}{r}$,AG=$\frac{2}{r}$$\sqrt{{r}^{2}-1}$,
∵∠AOG=∠COD,∠AGO=∠OCD,
∴△AGO∽△DCO,
∴$\frac{CD}{AG}$=$\frac{OC}{OG}$,
∴CD=$\frac{2r\sqrt{{r}^{2}-1}}{{r}^{2}-2}$.
点评 本题考查了切线的判定和性质,三角形的中位线的性质,勾股定理,线段垂直平分线的性质,直角三角形的性质,相似三角形的判定和性质等知识,熟练掌握应用所学知识是解题的关键.


科目:初中数学 来源: 题型:解答题
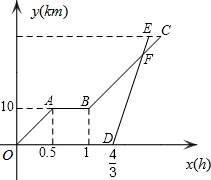 周末,甲、乙两人从学校出发去公园游玩,甲骑自行车出发0.5小时后到达苏果超市,在超市里休息了一段时间,再以相同的速度前往公园.乙因为一些事情耽搁了一些时间,在甲出发$\frac{4}{3}$小时后,乙驾驶电瓶车沿相同的路线前往公园,如图,是他们离学校的路程y(km)与行走的时间x(h)的函数图象.已知乙驾驶电瓶车的速度是甲骑自行车的2倍.
周末,甲、乙两人从学校出发去公园游玩,甲骑自行车出发0.5小时后到达苏果超市,在超市里休息了一段时间,再以相同的速度前往公园.乙因为一些事情耽搁了一些时间,在甲出发$\frac{4}{3}$小时后,乙驾驶电瓶车沿相同的路线前往公园,如图,是他们离学校的路程y(km)与行走的时间x(h)的函数图象.已知乙驾驶电瓶车的速度是甲骑自行车的2倍.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
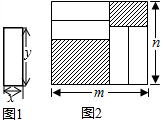 把四张形状大小完全相同的小长方形卡片(如图1)不重复地放在一个底面长为m厘米、宽为n厘米的长方形的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.
把四张形状大小完全相同的小长方形卡片(如图1)不重复地放在一个底面长为m厘米、宽为n厘米的长方形的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com