
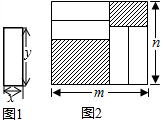
 把四张形状大小完全相同的小长方形卡片(如图1)不重复地放在一个底面长为m厘米、宽为n厘米的长方形的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.
把四张形状大小完全相同的小长方形卡片(如图1)不重复地放在一个底面长为m厘米、宽为n厘米的长方形的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.分析 (1)设小长方形卡片的宽为xcm,长为ycm,可得:m-y=2x,即2x+y=m,分别表示阴影部分两长方形的长与宽,进而表示出阴影部分的周长和,去括号合并后,将2x+y=m代入,即可得到结果.
(2)把n的值代入即可.
解答 解:(1)设小长方形卡片的宽为xcm,长为ycm,可得:m-y=2x,即2x+y=m,
根据题意得:阴影部分的周长为:
2m+2(n-y)+2(n-2x),
=2(m+n-y+n-2x),
=2[m+2n-(2x+y)],
=2(m+2n-m),
=4n(cm).
(2)当n=8厘米时,阴影部分的周长为4×8=32(厘米),
答:当n=8厘米时两块阴影部分的周长和32厘米.
点评 此题考查了整式加减运算的应用,弄清题意,表示出阴影部分的长和宽是解本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 8-4-6+5 | B. | 8-4-6-5 | C. | 8+(-4)+(-6)+5 | D. | 8+4-6-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在射线OM上有三点A、B、C.OA=20,AB=m,BC=n,m,n满足|m-6n|=-(10-n)2.点P从点O出发,沿OM方向以每秒1个单位的速度匀速运动.点Q从点C出发在线段CO上向点O匀速运动(点O运动到点O时停止运动).两点同时出发.
如图所示,在射线OM上有三点A、B、C.OA=20,AB=m,BC=n,m,n满足|m-6n|=-(10-n)2.点P从点O出发,沿OM方向以每秒1个单位的速度匀速运动.点Q从点C出发在线段CO上向点O匀速运动(点O运动到点O时停止运动).两点同时出发.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
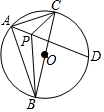 如图,⊙O是△ABC的外接圆,BC为直径,AD平分∠BAC交⊙O于D,点P为△ABC的内心,PD=5$\sqrt{2}$,AB=8.下列结论:
如图,⊙O是△ABC的外接圆,BC为直径,AD平分∠BAC交⊙O于D,点P为△ABC的内心,PD=5$\sqrt{2}$,AB=8.下列结论:| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
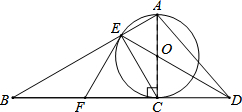 已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC中,BC=10,BC边上的高AH=8,四边形DEFG为内接矩形.
如图,已知△ABC中,BC=10,BC边上的高AH=8,四边形DEFG为内接矩形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com