
 如图,已知△ABC中,BC=10,BC边上的高AH=8,四边形DEFG为内接矩形.
如图,已知△ABC中,BC=10,BC边上的高AH=8,四边形DEFG为内接矩形.分析 (1)GF∥BC得△AGF∽△ABC,利用相似三角形对应边上高的比等于相似比,列方程求解.
(2)根据相似三角形的性质求出GF=10-$\frac{5}{4}$x,求出矩形的面积,运用二次函数性质解决问题.
解答 解:(1)设HK=y,则AK=AH-KH=AH-EF=8-y,
∵四边形DEFG为矩形,
∴GF∥BC,
∴△AGF∽△ABC,
∴AK:AH=GF:BC,
∵当矩形DEFG是正方形时,GF=KH=y,
∴8-y:8=y:10,
解得:y=$\frac{40}{9}$;
(2)设EF=x,则KH=x.
∴AK=AH-EF=8-x,
由(1)可知:$\frac{GF}{10}=\frac{8-x}{8}$,
解得:GF=10-$\frac{5}{4}$x,
∴s=GF•EF=(10-$\frac{5}{4}$x)x=-$\frac{5}{4}$(x-4)2+20,
∴当x=4时S有最大值,并求出最大值20.
点评 本题考查了相似三角形的性质,二次函数的最值,矩形的性质的应用,注意:矩形的对边相等且平行,相似三角形的对应高的比等于相似比,题目是一道中等题,难度适中.


科目:初中数学 来源: 题型:解答题
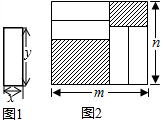 把四张形状大小完全相同的小长方形卡片(如图1)不重复地放在一个底面长为m厘米、宽为n厘米的长方形的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.
把四张形状大小完全相同的小长方形卡片(如图1)不重复地放在一个底面长为m厘米、宽为n厘米的长方形的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com