

分析 (1)当重叠部分为完整的△DEF的面积时,求出S△DEF=$\frac{1}{2}$CE•DF=$\frac{1}{2}$×5t×4t=10t2,即F与B重合时,是边界,列式10t2=10,可求出t=1,即a=1;
(2)分三种情况:①如图1,当0<t≤1时,S=S△DEF=10t2,②当1<t≤$\frac{3}{2}$时,如图5,重叠部分为△DEF和△BGF面积的差;③当D与B重合时,S=0,则c=8÷3=$\frac{8}{3}$,当$\frac{3}{2}$<t≤$\frac{8}{3}$时,如图6,重叠部分的面积为△BDG的面积.
解答 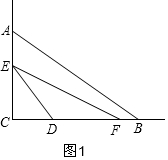 解:(1)由题意得:CD=3t,CE=4t,
解:(1)由题意得:CD=3t,CE=4t,
由勾股定理得:DE=5t,
∴DF=DE=5t,
∴S△DEF=$\frac{1}{2}$CE•DF=$\frac{1}{2}$×5t×4t=10t2,
当10t2=10时,
t=±1,
∴a=1,
故答案为:1;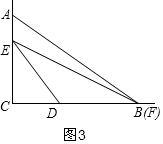
(2)由图2可知:当t=1时,△DEF与△ABC重叠部分的面积为△DEF的面积,
①如图1,当0<t≤1时,S=S△DEF=10t2,
如图3,当t=1时,此时F与B重合,
BC=CD+DF=3t+5t=8t=8
由图2可知:当t=$\frac{3}{2}$时,E与A重合,如图4
此时,AC=CE=4t=4×$\frac{3}{2}$=6,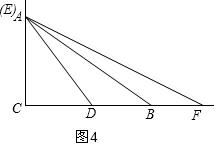
②当1<t≤$\frac{3}{2}$时,如图5,设EF与AB交于G,过G作GH⊥BC于H,
BF=CD+DF-BC=3t+5t-8=8t-8,
∵tan∠ABC=$\frac{AC}{BC}$=$\frac{GH}{BH}$=$\frac{6}{8}$=$\frac{3}{4}$,
∴设GH=3x,BH=4x,
tan∠EFC=$\frac{EC}{FC}=\frac{GH}{FH}$,
∴$\frac{4t}{8t}=\frac{GH}{FH}$=$\frac{1}{2}$,
∴FH=2GH,
∴BH+BF=2GH,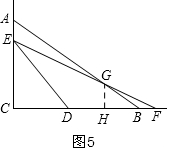
∴4x+8t-8=6x,
x=4t-4,
∴GH=3x=3(4t-4)=12t-12,
∴S=S△DEF-S△BGF=10t2-$\frac{1}{2}$BF•GH,
=10t2-$\frac{1}{2}$(8t-8)(12t-12),
=-38t2+96t-48,
③当D与B重合时,S=0,则c=8÷3=$\frac{8}{3}$,
当$\frac{3}{2}$<t≤$\frac{8}{3}$时,如图6,设ED与AB交于点G,过G作GH⊥BC于H,
同理设GH=3x,BH=4x,则DH=BH-BD=4x-(8-3t)=4x-8+3t,
tan∠GDH=$\frac{EC}{CD}=\frac{GH}{DH}$,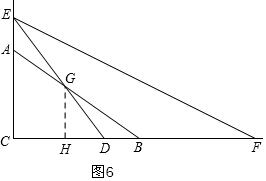
$\frac{4t}{3t}=\frac{3x}{4x-8+3t}$,
x=$\frac{32-12t}{7}$
∴GH=3x=$\frac{3(32-12t)}{7}$,
∴S=S△BDG=$\frac{1}{2}$BD•GH=$\frac{1}{2}$(8-3t)$•\frac{3(32-12t)}{7}$
=$\frac{54}{7}{t}^{2}$-$\frac{288}{7}$t+$\frac{384}{7}$;
综上所述,S与t的函数关系式为:
S=$\left\{\begin{array}{l}{10{t}^{2}(0<t≤1)}\\{-38{t}^{2}+96t-48(1<t≤\frac{3}{2})}\\{\frac{54}{7}{t}^{2}-\frac{288}{7}t+\frac{384}{7}(\frac{3}{2}<t≤\frac{8}{3})}\end{array}\right.$.
点评 本题是动点问题的函数图象,有难度,结合图1和图2认真理解题意,利用数形结合的思想,先表示出D和E的路程,根据已知条件分别求出直角△ABC两直角边的长是关键,并采用了分类讨论的思想,注意边界点的时间.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
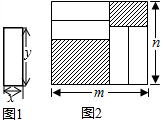 把四张形状大小完全相同的小长方形卡片(如图1)不重复地放在一个底面长为m厘米、宽为n厘米的长方形的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.
把四张形状大小完全相同的小长方形卡片(如图1)不重复地放在一个底面长为m厘米、宽为n厘米的长方形的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com