
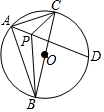
 如图,⊙O是△ABC的外接圆,BC为直径,AD平分∠BAC交⊙O于D,点P为△ABC的内心,PD=5$\sqrt{2}$,AB=8.下列结论:
如图,⊙O是△ABC的外接圆,BC为直径,AD平分∠BAC交⊙O于D,点P为△ABC的内心,PD=5$\sqrt{2}$,AB=8.下列结论:| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 连结PC、DC、BD,作PF⊥BC于F,PE⊥AC于E,PH⊥AB于H,根据内心的性质得∠ACP=∠BCP,根据圆周角定理由BC为直径得到∠BAC=90°,而AD平分∠BAC,则∠BAD=∠CAD=$\frac{1}{2}$∠BAC=45°,推出①成立,再次根据圆周角定理得到∠DBC=∠BCD=45°,于是可判断△BDC为等腰直角三角形,则BC=$\sqrt{2}$DC,然后利用三角形外角性质证明∠DPC=∠DCP得到DC=DP,推出②不成立,所以有BC=$\sqrt{2}$DP,推出③成立,由DP=5 $\sqrt{2}$得到BC=10,根据勾股定理计算出AC=6,根据切线长定理可计算出△ABC的内切圆半径为r=2,由此即可求出△APC的面积,即可判断④成立.
解答 证明:连结PC、DC、BD,作MF⊥BC于F,PE⊥AC于E,PH⊥AB于H,如图,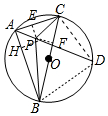
∵点P为△ABC的内心,
∴PC平分∠ACB,
∴∠ACP=∠BCP,
∵BC为直径,
∴∠BAC=90°,
∵AD平分∠BAC,
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC=45°,故①正确,
∴∠DBC=∠BCD=45°,
∴△BDC为等腰直角三角形,
∴BC=$\sqrt{2}$DC,
又∵∠DPC=∠PAC+∠ACP=45°+∠ACP,
而∠DCP=∠BCD+∠BCP,
∴∠DPC=∠DCP,
∴DC=DP=BD,
假设②正确,则△PDB是等边三角形,
∴∠ADB=60°=∠ACB,显然不可能,
故②错误.
∴BC=$\sqrt{2}$DP,即PD=$\frac{\sqrt{2}}{2}$BC,故③正确,
∵DP=5 $\sqrt{2}$,
∴BC=$\sqrt{2}$DP=10,
而AB=8,
∴AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=6,
设△ABC的内切圆半径为r,
∵点P为△ABC的内心,
∴PH=PE=PF=r,
∴四边形AHME为正方形,
∴AH=AE=r,则CE=CF=6-r,BH=BF=8-r,
而BF+FC=BC,
∴8-r+6-r=10,解得r=2,
∴S△APC=$\frac{1}{2}$•AC•PE=$\frac{1}{2}$×6×2=6,故④正确,
故正确的有①③④,
故选B.
点评 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了圆周角定理和勾股定理.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
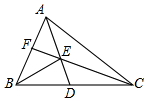 如图,△ABC中,E为AD与CF的交点,AE=ED,已知三角形ABC面积是1,三角形BEF的面积是$\frac{1}{10}$.求:
如图,△ABC中,E为AD与CF的交点,AE=ED,已知三角形ABC面积是1,三角形BEF的面积是$\frac{1}{10}$.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
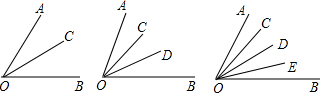
| ∠AOB内射线的条数 | 1 | 2 | 3 | 4 |
| 角的总个数 | 3 | 6 | 10 | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
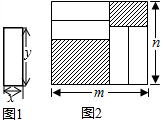 把四张形状大小完全相同的小长方形卡片(如图1)不重复地放在一个底面长为m厘米、宽为n厘米的长方形的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.
把四张形状大小完全相同的小长方形卡片(如图1)不重复地放在一个底面长为m厘米、宽为n厘米的长方形的盒子底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com