
| ∠AOB内射线的条数 | 1 | 2 | 3 | 4 |
| 角的总个数 | 3 | 6 | 10 | 15 |
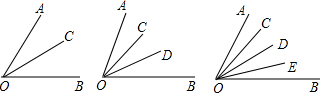
分析 (1)(2)若∠AOB内射线的条数是n,可构成$\frac{1}{2}$(n+1)(n+2)个角,依据规律回答即可;
(3)可设∠AOB内有射线条数x条,根据等量关系:角的总个数=5050个,列出方程求解即可.
解答 解:(1)填表如下:
| ∠AOB内射线的条数 | 1 | 2 | 3 | 4 |
| 角的总个数 | 3 | 6 | 10 | 15 |
点评 本题主要考查的是角的概念,掌握其规律是解题的关键.有公共顶点的n条射线,一共可构成$\frac{1}{2}$n(n-1)个角.


科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
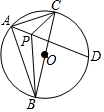 如图,⊙O是△ABC的外接圆,BC为直径,AD平分∠BAC交⊙O于D,点P为△ABC的内心,PD=5$\sqrt{2}$,AB=8.下列结论:
如图,⊙O是△ABC的外接圆,BC为直径,AD平分∠BAC交⊙O于D,点P为△ABC的内心,PD=5$\sqrt{2}$,AB=8.下列结论:| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
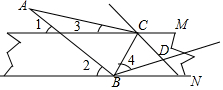 如图,一两边平行的纸条,将一直角三角板的直角顶点B放在纸片的一条边上,将三角板的另一个角的顶点C放在纸片的另一边上,∠ABC=90°,∠A=30°.
如图,一两边平行的纸条,将一直角三角板的直角顶点B放在纸片的一条边上,将三角板的另一个角的顶点C放在纸片的另一边上,∠ABC=90°,∠A=30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com