
 (1)解分式方程:
(1)解分式方程: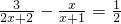 .
. ,
, 时,2(x+1)≠0,
时,2(x+1)≠0, ;
; CE,
CE, CE,
CE, ,
, CE,然后求出BC=ED,利用“边角边”证明△ABC和△CED全等,根据全等三角形对应角相等可得∠ABC=∠CED,再根据同位角相等,两直线平行证明即可.
CE,然后求出BC=ED,利用“边角边”证明△ABC和△CED全等,根据全等三角形对应角相等可得∠ABC=∠CED,再根据同位角相等,两直线平行证明即可.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com