练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．利用5×5方格作出面积为17的正方形．

    分析 已知图形是单位长度是1的网格，面积为17的正方形的边长为$\sqrt{17}$，由勾股定理得出$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$，容易作出面积为17的正方形．

    解答 解：由勾股定理得：$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$，
    四边形ABCD即为所求的面积为17的正方形，
    如图所示．

    点评 本题考查了勾股定理、正方形的性质；熟练掌握勾股定理，并能进行推理作图是解决问题的关键

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．填空
    （1）$\frac{ab}{{a}^{2}}=\frac{b}{（）}$；
    （2）$\frac{{x}^{3}}{{x}^{2}+xy}=\frac{（）}{x+y}$；
    （3）$\frac{x+y}{xy}=\frac{{x}^{2}+xy}{（）}$；
    （4）$\frac{x+y}{x-y}=\frac{（）}{{x}^{2}-2xy+{y}^{2}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

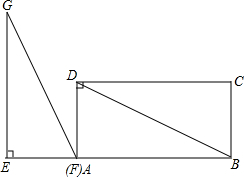    1．如图，在矩形ABCD中，DB=6，AD=3，在Rt△EFG中，∠GEF=90°，EF=3，GF=6，△EFG（点F和点A重合）的边EF和矩形的边AB在同一直线上．现Rt△EFG将从A以每秒1个单位的速度向射线AB方向匀速平移，当点F与点B重合时停止运动，设运动时间为t秒，解答下列问题：
    （1）当△EFG运动到$\sqrt{3}$秒时，GF经过点D；
    （2）在整个运动过程中，设△EFG与△ABD重叠部分面积为S，请直接写出S与t的函数关系式和相应t的取值范围；
    （3）当点F到达点B时，将△EFG绕点F顺时针旋转α（0＜α＜180°），旋转过程中EG所在直线交CD所在直线于M，交直线DB所在直线于点N，是否存在这样的α，使△DNM为等腰三角形？若存在，求DM的长，并直接写出答案；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．清晨，小强沿着一个如图所示的六边形广场周围的小路，按顺时针方向跑步
    （1）此六边形的内角和是多少？
    （2）他每跑完一圈，身体转过的角度之和为多少？
    （3）如果广场是七边形、八边形的形状，（2）中的结论还成立吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算：
    （1）$\root{3}{（-5）^{3}}$×（-$\frac{1}{5}$）2-$\sqrt{（-3）^{2}}$+$\root{3}{-\frac{8}{27}}$÷（$\frac{1}{3}$）2
    （2）-|3-$\sqrt{10}$|-|$\sqrt{10}$-$\sqrt{11}$|-|$\sqrt{11}$-$\sqrt{12}$|

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．在平面直角坐标系内点（x，y）满足x=y2，则点（x，y）位于（　　）
    A．x轴上方（含x轴）B．x轴下方（含x轴）C．y轴右方（含y轴）D．y轴左方（含y轴）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．计算：（3$\sqrt{5}$-2$\sqrt{3}$）（$\sqrt{18}$+$\sqrt{20}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．已知$\left\{\begin{array}{l}{x=3}\\{y=-4}\end{array}\right.$是方程ax-2y=2的一个解，则a的值为（　　）
    A．-2B．2C．$\frac{10}{3}$D．-$\frac{10}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．青山村种的水稻2009年平均每公顷产7500千克，2011年平均每公顷产9075千克，求水稻每公顷产量的年平均增长率．

    查看答案和解析>>

    同步练习册答案