练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
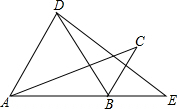
    10．如图，将△ABC绕点B顺时针旋转60°得△DBE，点C的对应点E恰好落在AB延长线上，连接AD．下列结论一定正确的是（　　）
    A．∠ABD=∠EB．∠CBE=∠CC．AD∥BCD．AD=BC

    分析 由旋转的性质得到∠ABD=∠CBE=60°，AB=BD，推出△ABD是等边三角形，得到∠DAB=∠CBE，于是得到结论．

    解答 解：∵△ABC绕点B顺时针旋转60°得△DBE，
    ∴∠ABD=∠CBE=60°，AB=BD，
    ∴△ABD是等边三角形，
    ∴∠DAB=60°，
    ∴∠DAB=∠CBE，
    ∴AD∥BC，
    故选C．

    点评 本题考查了旋转的性质，等边三角形的判定和性质，平行线的判定，熟练掌握旋转的性质是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    20．如图，点A在以BC为直径的⊙O内，且AB=AC，以点A为圆心，AC长为半径作弧，得到扇形ABC，剪下扇形ABC围成一个圆锥（AB和AC重合），若∠BAC=120°，BC=4$\sqrt{3}$，则圆锥底面圆的半径是（　　）
    A．$\frac{4}{3}$B．$\frac{2}{3}$C．$\sqrt{3}$D．$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

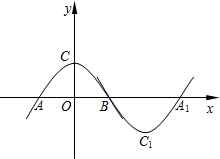    1．如图所示，抛物线l1：y=ax2+b（a＜0，b＞0）与x轴交于点A、B（点A在点B的左侧），与y轴交于点C，将抛物线l1绕点B旋转180°，得到新的抛物线l2，它的顶点为C1，与x轴的另一个交点为A1
    （1）当a=-1，b=1时，求B点坐标及抛物线l2的解析式；
    （2）若a=-$\frac{1}{2}$，且四边形AC1A1C为矩形，求抛物线l1的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

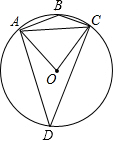    18．如图，⊙O是四边形ABCD的外接圆，连接AC，OA，OC，若∠ABC：∠ACO=13：4，则∠ADC的度数为（　　）
    A．30°B．50°C．40°D．45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，已知△ABC内接于⊙O，点C在劣弧AB上（不与点A，B重合），点D为弦BC的中点，DE⊥BC，DE与AC的延长线交于点E，射线AO与射线EB交于点F，与⊙O交于点G，设∠GAB=ɑ，∠ACB=β，∠EAG+∠EBA=γ，
    （1）点点同学通过画图和测量得到以下近似数据：
    ɑ30°40°50°60°
    β120°130°140°150°
    γ150°140°130°120°
    猜想：β关于ɑ的函数表达式，γ关于ɑ的函数表达式，并给出证明：
    （2）若γ=135°，CD=3，△ABE的面积为△ABC的面积的4倍，求⊙O半径的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

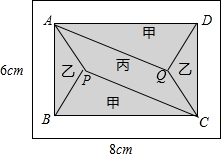    15．小黄准备给长8m，宽6m的长方形客厅铺设瓷砖，现将其划分成一个长方形ABCD区域Ⅰ（阴影部分）和一个环形区域Ⅱ（空白部分），其中区域Ⅰ用甲、乙、丙三种瓷砖铺设，且满足PQ∥AD，如图所示．
    （1）若区域Ⅰ的三种瓷砖均价为300元/m2，面积为S（m2），区域Ⅱ的瓷砖均价为200元/m2，且两区域的瓷砖总价为不超过12000元，求S的最大值；
    （2）若区域Ⅰ满足AB：BC=2：3，区域Ⅱ四周宽度相等
    ①求AB，BC的长；
    ②若甲、丙两瓷砖单价之和为300元/m2，乙、丙瓷砖单价之比为5：3，且区域Ⅰ的三种瓷砖总价为4800元，求丙瓷砖单价的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图1所示，在△ABC中，点O是AC上一点，过点O的直线与AB，BC的延长线分别相交于点M，N．
    【问题引入】
    （1）若点O是AC的中点，$\frac{AM}{BM}$=$\frac{1}{3}$，求$\frac{CN}{BN}$的值；
    温馨提示：过点A作MN的平行线交BN的延长线于点G．
    【探索研究】
    （2）若点O是AC上任意一点（不与A，C重合），求证：$\frac{AM}{MB}$•$\frac{BN}{NC}$•$\frac{CO}{OA}$=1；
    【拓展应用】
    （3）如图2所示，点P是△ABC内任意一点，射线AP，BP，CP分别交BC，AC，AB于点D，E，F，若$\frac{AF}{BF}$=$\frac{1}{3}$，$\frac{BD}{CD}$=$\frac{1}{2}$，求$\frac{AE}{CE}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

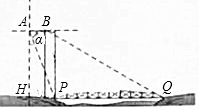    19．如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的
    俯角为α其中tanα=2$\sqrt{3}$，无人机的飞行高度AH为500$\sqrt{3}$米，桥的长度为1255米．
    ①求点H到桥左端点P的距离；  
    ②若无人机前端点B测得正前方的桥的右端点Q的俯角为30°，求这架无人机的长度AB．

    查看答案和解析>>

    科目：初中数学 来源：2017届江苏省启东市九年级寒假作业测试（开学考试）数学试卷（解析版） 题型：解答题

    已知：如图△ABC三个顶点的坐标分别为A（0，﹣3）、B（3，﹣2）、C（2，﹣4），正方形网格中，每个小正方形的边长是1个单位长度．

    （1）画出△ABC向上平移6个单位得到的△A1B1C1；

    （2）以点C为位似中心，在网格中画出△A2B2C2，使△A2B2C2与△ABC位似，且△A2B2C2与△ABC的位似比为2：1，并直接写出点A2的坐标．

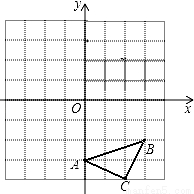
    查看答案和解析>>

    同步练习册答案