
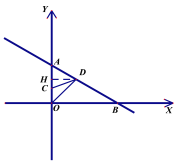
【题目】如图,直线![]() 图像与y轴、x轴分别交于A、B两点
图像与y轴、x轴分别交于A、B两点
(1)求点A、B坐标和∠BAO度数
(2)点C、D分别是线段OA、AB上一动点(不与端点重合),且CD=DA,设线段OC的长度为x ,![]() ,请求出y关于x的函数关系式以及定义域
,请求出y关于x的函数关系式以及定义域
(3)点C、D分别是射线OA、射线BA上一动点,且CD=DA,当ΔODB为等腰三角形时,求C的坐标(第(3)小题直接写出分类情况和答案,不用过程)



【答案】(1)A(0,3),B(![]() ),60°(2)
),60°(2)![]() (0<x<3)(3)(0,0),
(0<x<3)(3)(0,0),![]() ,(0,6)
,(0,6)
【解析】
(1)对于一次函数解析式,分别令x与y为0求出对应的y与x的值,得到A、B两点坐标,然后再根据三角函数求出∠BAO的度数即可;
(2)先证明△ACD是等边三角形,根据等边三角形的性质可得AD=CD=AC=3-x,作DH⊥y轴于点H,用含x的式子表示出DH的长,然后根据三角形面积公式进行求解即可;
(3)当△ODB为等腰三角形时,分三种情况讨论:当OD=DB时;当BD=BO时;当OD=OB时,利用等边三角形的性质分别求出C点坐标即可.
(1)一次函数![]() ,
,
令![]() ,则有
,则有![]() ,解得:
,解得:![]() ,
,![]() ,
,
令![]() ,得
,得![]() ,
,![]() ,
,
![]() ,
,
在![]()
![]() ,
,![]() ,
,
∵sin∠ABO=![]() ,
,
![]() ,
,
![]() ;
;
(2)过点D作DH⊥y轴,垂足为点H,
![]() ,
,
![]() ,
,
![]() ,
,
∴ΔADC是等边三角形,
![]() ,
,![]() ,
,
![]()
![]() =
=![]() =
=![]() ,
,
∵S△OCD=![]() ,
,
![]() ;
;
(3)由(1)知,在Rt△OAB中,OA=3,OB=3![]() ,∠BAO=60°,AB=6,∠ABO=30°,
,∠BAO=60°,AB=6,∠ABO=30°,
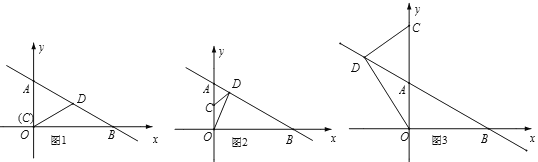
当△ODB为等腰三角形时,分三种情况进行讨论:
①如图1,当OD=DB时,D在OB的垂直平分线上,则D为AB的中点,AD=![]() AB=3,
AB=3,
∵CD=DA,∠CAD=60°,
∴△ACD是等边三角形,
∴AC=AD=3,
∴C与原点重合,
∴C点坐标为(0,0);
②如图2,当BD=BO=3![]() 时,AD=AB-BD=6-3
时,AD=AB-BD=6-3![]() ,
,
∵CD=DA,∠CAD=60°,
∴△ACD是等边三角形,
∴AC=AD=6-3![]() ,
,
∴OC=OA-AC=3-(6-3![]() )=3
)=3![]() -3,
-3,
∴C点坐标为(0,3![]() -3);
-3);
③如图3,当OD=OB=3![]() 时,∠ODB=∠OBD=30°,
时,∠ODB=∠OBD=30°,
∵∠AOD=∠BAO-∠ODB=60°-30°,
∴∠ODB=∠AOD=30°,
∴AD=OA=3,
∵CD=DA,∠CAD=60°,
∴△ACD是等边三角形,
∴AC=AD=3,
∴OC=OA+AC=3+3=6,
∴C点坐标为(0,6),
综上,点C的坐标为(0,0),![]() ,(0,6).
,(0,6).


科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每一个小正方形的边长为1.△ABC的三个顶点都在格点上,A、C的坐标分别是(﹣4,6),(﹣1,4).
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC向右平移6个单位的△A1B1C1,并写出C1的坐标 ;
(3)请画出△ABC关于原点O对称的△A2B2C2 , 并写出点C2的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在一条不完整的数轴上一动点A向左移动4个单位长度到达点B,再向右移动7个单位长度到达点C.
![]()
(1)若点A表示的数为0,求点B、点C表示的数;
(2)若点C表示的数为5,求点B、点A表示的数;
(3)如果点A、C表示的数互为相反数,求点B表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某校组织的初中数学应用能力竞赛中,每班参加比赛的人数相同,成绩分为A、B、C、D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将八年级的一班和二班的成绩整理并绘制成如下的统计图,二班D级共有4人.

请你根据以上提供的信息解答下列问题:
(1)求此竞赛中一班共有多少人参加比赛,并补全条形统计图.
(2)扇形统计图中A级对应的圆心角度数是 .
(3)此次竞赛中二班在C级以上(包括C级)的人数为 .
(4)请你将表格补充完成:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号里:
﹣5.![]() ,|﹣
,|﹣![]() |,0.5252252225…,0,﹣0.6363,﹣(﹣1)2007,1
|,0.5252252225…,0,﹣0.6363,﹣(﹣1)2007,1![]() ,23%,﹣π
,23%,﹣π
正数集合:{ }
负数集合:{ }
整数集合:{ }
分数集合:{ }
无理数集合:{ }
非负数集合:{ }
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图要求:Ⅰ、过直线外一点作这条直线的垂线;Ⅱ、作线段的垂直平分线;
Ⅲ、过直线上一点作这条直线的垂线;Ⅳ、作角的平分线.
如图是按上述要求排乱顺序的尺规作图:

则正确的配对是( )
A. ①﹣Ⅳ,②﹣Ⅱ,③﹣Ⅰ,④﹣Ⅲ B. ①﹣Ⅳ,②﹣Ⅲ,③﹣Ⅱ,④﹣Ⅰ
C. ①﹣Ⅱ,②﹣Ⅳ,③﹣Ⅲ,④﹣Ⅰ D. ①﹣Ⅳ,②﹣Ⅰ,③﹣Ⅱ,④﹣Ⅲ
查看答案和解析>>
科目:初中数学 来源: 题型:
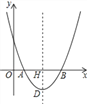
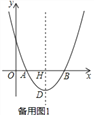
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣10ax+16a(a≠0)交x轴于A、B两点,抛物线的顶点为D,对称轴与x轴交于点H,且AB=2DH.
(1)求a的值;
(2)点P是对称轴右侧抛物线上的点,连接PD,PQ⊥x轴于点Q,点N是线段PQ上的点,过点N作NF⊥DH于点F,NE⊥PD交直线DH于点E,求线段EF的长;
(3)在(2)的条件下,连接DN、DQ、PB,当DN=2QN(NQ>3),2∠NDQ+∠DNQ=90°时,作NC⊥PB交对称轴左侧的抛物线于点C,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简求值:
(1)当a=﹣1,b=2时,求代数式﹣2(ab﹣3b2)﹣[6b2﹣(ab﹣a2)]的值
(2)先化简,再求值:4xy﹣2(![]() x2﹣3xy+2y2)+3(x2﹣2xy),当(x﹣3)2+|y+1|=0,求式子的值
x2﹣3xy+2y2)+3(x2﹣2xy),当(x﹣3)2+|y+1|=0,求式子的值
(3)若(2mx2﹣x+3)﹣(3x2﹣x﹣4)的结果与x的取值无关,求m的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com