练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一名足球守门员练习折返跑，从球门线出发，向前记作正数，返回记作负数，他的记录如下：（单位：米）+5，-3，+10，-8，-6，+12，-10

    （1）守门员最后是否回到了球门线的位置？

    （2）在练习过程中，守门员离开球门最远距离是多少米？

    （3）守门员全部练习结束后，他共跑了多少米？

    【答案】（1）回到了球门线的位置（2 ）12米（3）58米

    【解析】试题分析：（1）将各数进行相加，看结果是否为零，如果结果为零就说明回到了球门线的位置；（2）根据有理数的加法计算法则求出每次离球门线的距离，然后进行比较大小；（3）将各数的绝对值进行相加，得出答案．

    试题解析：⑴、（+5）+（-3）+（+10）+（-8）+（-6）+（+12）+（-10）=0,

    ∴守门员最后正好回到了球门线的位置．

    ⑵、5+（－3）=2 2+10=12 12+（－8）=4 4+（－6）=－2 －2+12=10 10+（－10）=0

    ∴守门员离开球门线距离最远是12米．

    ⑶、=54

    答：他共跑了54米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】北方某水果商店从南方购进一种水果，其进货成本是每吨0.4万元，根据市场调查，这种水果在北方市场上的销售量为 y(吨)，销售价 x( 万元)之间的函数关系为y=-x+2.6.

    (1)当每吨销售价为多少万元时，销售利润为 0.96万元?

    (2)填空 当每吨销售价为 万元时，可得最大利润为 万元.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=5，OC=4．在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，边AE上有一动点P（不与A，E重合）自A点沿AE方向向E点匀速运动，运动的速度为每秒1个单位长度，设运动的时间为t秒（0＜t＜5），过P点作ED的平行线交AD于点M，过点M作AE的平行线交DE于点N．

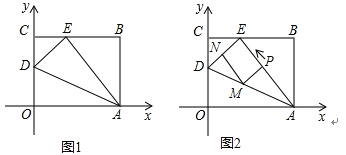
    （1）直接写出 D，E 两点的坐标，D（ ），E（ ）

    （2）求四边形PMNE的面积S与时间t之间的函数关系式；当t取何值时，S有最大值？

    （3）当t为何值时，DP平分∠EDA？

    （4）当t为何值时，以A，M，E为顶点的三角形为等腰三角形，并求出相应的时刻点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】回答下列问题：

    （1）如图所示的甲、乙两个平面图形能折成什么几何体？________________．

    （2）由多个平面围成的几何体叫做多面体．若一个多面体的面数为，顶点个数为，棱数为，分别计算第（1）题中两个多面体的的值？你发现什么规律？

    （3）应用上述规律解决问题：一个多面体的顶点数比面数大8，且有50条棱，求这个几何体的面数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某果品批发公司以16元/千克购进一批樱桃．由往年市场销售情况的统计分析可知：当销售价定为25 元/千克时，每天可售出1 000 千克；若销售价定为20元/千克时，每天可售出2000千克．假设每天的销售量y（千克）与销售价x（元/千克）之间满足一次函数．

    （1）试求y与x之间的函数关系式；

    （2）在商品无积压且不考虑其他因素的条件下，销售价格定为多少时，才能使每天的销售毛利润W（元）最大？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 “十一”黄金周期间，西安大唐芙蓉园在7天假期中每天接待游客的人数变化如下表（正数表示比前一天多的人数，负数表示比前一天少的人数）。

    日期

    10月1日

    10月2日

    10月3日

    10月4日

    10月5日

    10月6日

    10月7日

    人数变化

    （万人）

    +1．6

    +0．8

    +0．4

    -0．4

    -0．8

    +0．2

    -1．4

    （1）若9月30日的游客人数为万人，则10月2日的游客人数为_______万人；

    （2）七天内游客人数最大的是10月_______日；

    （3）若9月30日游客人数为3万人，门票每人120元。请求出黄金周期间西安大唐芙蓉园门票总收入是多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店积压了100件某种商品，为使这批货物尽快脱手，该商店采取了如下销售方案，将价格提高到原来的2．5倍，再作3次降价处理；第一次降价30％，标出“亏本价”；第二次降价30％，标出“破产价”；第三次降价30%，标出“跳楼价”．3次降价处理销售结果如下表：

    降价次数

    一

    二

    三

    销售件数

    10

    40

    一抢而光

    （1）跳楼价占原价的百分比是多少?

    （2）该商品按新销售方案销售，相比原价全部售完，哪种方案更盈利?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1是立方体和长方体模型，立方体棱长和长方体底面各边长都为1，长方体侧棱长为2，现用60张长为6，宽为4的长方形卡纸，剪出这两种模型的表面展开图，有两种方法：

    方法一：如图2，每张卡纸剪出3个立方体表面展开图；

    方法二：如图3，每张卡纸剪出2个长方体表面展开图（图中只画出1个）．

    设用x张卡纸做立方体，其余卡纸做长方体，共做两种模型y个．要求制作的长方体的个数不超过立方体的个数．

    （1）在图3中画出第二个长方体表面展开图，用阴影表示；

    （2）请你写出y关于x的函数解析式，并注明自变量x的取值范围；

    （3）设每只模型（包括立方体和长方体）平均获利为w（元），w满足函数，

    若想将模型作为教具卖出获得最大利润，则应该制作立方体和长方体各多少个？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】

    （1）甲、乙多少秒后相遇？

    （2）甲出发多少秒后，甲到A、B、C三点的距离和为40个单位？

    （3）当甲到A、B、C三点的距离和为40个单位时，甲调头返回，当甲、乙在数轴上再次相遇时，相遇点表示的数是 ．

    查看答案和解析>>

    同步练习册答案