
【题目】

(1)甲、乙多少秒后相遇?
(2)甲出发多少秒后,甲到A、B、C三点的距离和为40个单位?
(3)当甲到A、B、C三点的距离和为40个单位时,甲调头返回,当甲、乙在数轴上再次相遇时,相遇点表示的数是 .
【答案】(1)甲、乙3.4秒后相遇;(2)甲出发2或5秒后,甲到A、B、C三点的距离和为40个单位;(3)﹣44.
【解析】试题分析:(1)可设x秒后甲与乙相遇,根据相遇时甲与乙所行路程之和为34列出方程,求解即可;
(2)设y秒后甲到A,B,C三点的距离之和为40个单位,分甲应为于AB或BC之间两种情况讨论即可求解;
(3)设z秒后甲、乙在数轴上再次相遇,那么此时甲、乙表示在数轴上为同一点,依此列出方程求解即可.
解:(1)设x秒后甲与乙相遇,则
4x+6x=34,
解得x=3.4,
答:甲、乙3.4秒后相遇;
(2)设y秒后甲到A,B,C三点的距离之和为40个单位,
B点距A,C两点的距离为14+20=34<40,A点距B、C两点的距离为14+34=48>40,C点距A、B的距离为34+20=54>40,故甲应为于AB或BC之间.
①AB之间时:4y+(14﹣4y)+(14﹣4y+20)=40,解得y=2;
②BC之间时:4y+(4y﹣14)+(34﹣4y)=40,解得y=5.
答:甲出发2或5秒后,甲到A、B、C三点的距离和为40个单位;
(3)①甲从A向右运动2秒时返回,设z秒后与乙再次相遇.此时甲、乙表示在数轴上为同一点,所表示的数相同.
甲表示的数为:﹣24+4×2﹣4z;乙表示的数为:10﹣6×2﹣6z,
依据题意得:﹣24+4×2﹣4z=10﹣6×2﹣6z,
解得:z=7,
相遇点表示的数为:﹣24+4×2﹣4z=﹣44(或:10﹣6×2﹣6z=﹣44),
②甲从A向右运动5秒时返回,设y秒后与乙相遇.
甲表示的数为:﹣24+4×5﹣4z;乙表示的数为:10﹣6×5﹣6z,
依据题意得:﹣24+4×5﹣4z=10﹣6×5﹣6z,
解得:z=﹣8(不合题意舍去),
答:当甲、乙在数轴上再次相遇时,相遇点表示的数为﹣44.
故答案为﹣44.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.
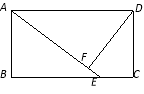
(1)△ABE与△ADF相似吗?请说明理由.
(2)若AB=6,AD=12,BE=8,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】识图理解:
请认真观察如图给出的未来一周某市的每天的最高气温和最低气温,直接回答后面提出的问题:
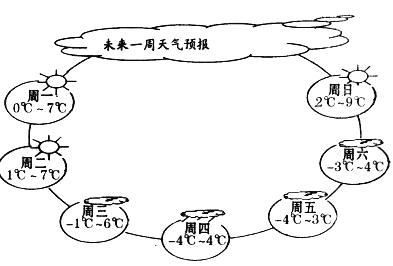
(1)这一周该市的最高气温和最低气温分别是多少?
(2)这一周中,星期几的温差最大?是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值 (单位:g) |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)这批样品的平均质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?

(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com