
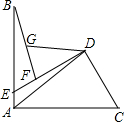
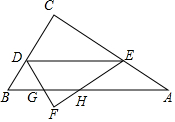
 已知:AB=AC,DC=DF,∠BAC=∠CDF=90°,点G在BF上,
已知:AB=AC,DC=DF,∠BAC=∠CDF=90°,点G在BF上,分析 (1)如图,延长AG到M使得GM=AG,连接BM、AF、DA、DM,延长MF交AB于N.只要证明△ACD≌△MFD,即可推出DM=AD,∠ADC=∠MDF,推出∠MDA=∠FDC=90°,推出△ADM是等腰直角三角形,由AG=GM,推出AG⊥DG AG=DG.
(2)如图2中,过点A作AM⊥AD交DG的延长线于M,连接MB延长MB交CD的延长线于N,连接MF、BD、AF、AD.只要证明△MAB≌△DAC,四边形BDFM是平行四边形,即可解决问题.
解答 证明:(1)如图,延长AG到M使得GM=AG,连接BM、AF、DA、DM,延长MF交AC于N.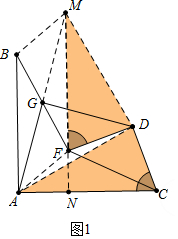
∵BG=GF,AG=GM,
∴四边形ABMF是平行四边形,
∴AB=MF=AC,AB∥MN,
∴∠MNC=∠BAC=90°,
∴∠FNC+∠FDC=180°,
∴∠DFN+∠NCD=180°,∵∠MFD+∠DFN=180°,
∴∠MFD=∠ACD,
在△ACD和△MFD中,
$\left\{\begin{array}{l}{AC=MF}\\{∠ACD=∠MFD}\\{CD=DF}\end{array}\right.$,
∴△ACD≌△MFD,
∴DM=AD,∠ADC=∠MDF,
∴∠MDA=∠FDC=90°,
∴△ADM是等腰直角三角形,∵AG=GM,
∴AG⊥DG AG=DG.
(2)如图2中,过点A作AM⊥AD交DG的延长线于M,连接MB延长MB交CD的延长线于N,连接MF、BD、AF、AD.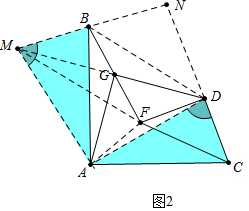
∵∠MAD=90°,∠ADM=45°,
∴∠AMD=∠ADM=45°,
∴AM=AD,
∵∠AMD=∠BAC,
∴∠MAB=∠CAD,∵AM=AD,AB=AC,
∴△MAB≌△DAC,
∴BM=CD=DF,∠AMB=∠ADC,
∵∠ADC+∠ADN=180°,
∴∠AMB+∠ADN=180°,
∴∠MAD+∠N=180°,
∴∠N=∠FDC=90°,
∴NM∥DF,
∴四边形BDFM是平行四边形,
∴BG=FG.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质和判定、平行四边形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造特殊四边形或全等三角形解决问题,题目比较难,辅助线比较多.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.65×109 | B. | 4.65×1010 | C. | 4.65×1011 | D. | 4.65×1012 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
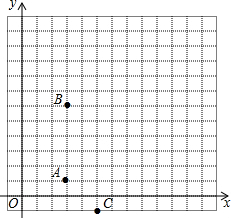 某城市的街道恰好呈东西与南北横纵交错格局(如图所示),一次,警察局电子监控器屏幕上发现一辆作案后的小轿车正在点A(3,1)处以每分钟0.5个单位长度的速度向北逃窜,根据各街道的交通状况进行分析,逃犯很可能逃到点B(3,6)后改为向东逃窜,此时正在点C(5,-1)处巡逻的警车接到指令后立即以每分钟0.7个单位长度的速度进行追捕,逃犯将在什么地方被追捕到?
某城市的街道恰好呈东西与南北横纵交错格局(如图所示),一次,警察局电子监控器屏幕上发现一辆作案后的小轿车正在点A(3,1)处以每分钟0.5个单位长度的速度向北逃窜,根据各街道的交通状况进行分析,逃犯很可能逃到点B(3,6)后改为向东逃窜,此时正在点C(5,-1)处巡逻的警车接到指令后立即以每分钟0.7个单位长度的速度进行追捕,逃犯将在什么地方被追捕到?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
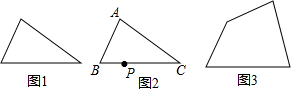
 直角三角形ABC中,∠C=90度,CB=6,AC=8,D为CB边上一个动点,E为AC上一点,DE∥AB,将三角形CDE沿着DE翻折得到三角形DEF,设三角形DEF和三角形ABC重合的面积为y,DC=x,求y与x的函数关系式及定义域.
直角三角形ABC中,∠C=90度,CB=6,AC=8,D为CB边上一个动点,E为AC上一点,DE∥AB,将三角形CDE沿着DE翻折得到三角形DEF,设三角形DEF和三角形ABC重合的面积为y,DC=x,求y与x的函数关系式及定义域.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
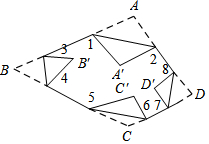 如图所示,把一个四边形纸片ABCD的四个顶角分别向内折叠,折叠之后,4个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8的度数是720°.
如图所示,把一个四边形纸片ABCD的四个顶角分别向内折叠,折叠之后,4个顶点不重合,那么图中∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8的度数是720°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com