
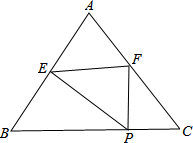
 如图,在△ABC中,AB=AC=5,BC=6,点P时边BC上一动点,过点P作PF⊥BC交AC于F,作PE⊥AB于E.
如图,在△ABC中,AB=AC=5,BC=6,点P时边BC上一动点,过点P作PF⊥BC交AC于F,作PE⊥AB于E.分析 (1)分三种情况:①当PE=PF时,过A作AD⊥BC于D,于是得到CD=BD=$\frac{1}{2}$BC,设PE=PF=x,通过△CFP∽△CAD于是得到CP=$\frac{9}{4}$;②当EF=EP时,∠EPF=∠EFP,通过△EFP∽△ABC,设CP=x,则PF=$\frac{4}{3}$x,EP=$\frac{4}{5}$(6-x),得到$\frac{PE}{AB}=\frac{FP}{BC}$,即$\frac{\frac{4}{5}(6-x)}{5}=\frac{\frac{4}{3}x}{6}$,于是得到CP=$\frac{108}{43}$;③当EF=FP时,过F作FM⊥EP于M,设PC=x,通过△FMP∽△ADC,得到$\frac{FP}{PM}=\frac{AC}{AD}=\frac{5}{4}$,于是得到PC=$\frac{18}{11}$,
(2)①当EF∥BC时,△EFP是直角三角形,设PC=x,则CF=$\frac{5}{3}$x,PF=$\frac{4}{3}$x,EF=$\frac{16}{9}$x,根据平行线分线段成比例定理得到$\frac{EF}{BC}=\frac{AF}{AC}$,于是求得PC=$\frac{27}{17}$,②当点F,A重合时,△EFP是直角三角形,此时PC=3.
解答 解:(1)①当PE=PF时,过A作AD⊥BC于D,∴CD=BD=$\frac{1}{2}$BC,
∵AB=AC=5,BC=6,
∴CD=3,AD=4,
在△PBE与△PCF中,$\left\{\begin{array}{l}{∠PEB=∠FPC=90°}\\{∠B=∠C}\\{PE=PF}\end{array}\right.$,
∴△PBE≌△PCF,
∴PB=CF,
设PE=PF=x,
∵PF⊥BC,
∴AD∥PF,
∴△CFP∽△CAD,
∴$\frac{FP}{AD}=\frac{CP}{CD}=\frac{CF}{AC}$,
∴PC=$\frac{3}{4}$x,CF=$\frac{5}{4}$x,
∴PC+CF=$\frac{3}{4}$x+$\frac{5}{4}$x=6,
∴x=3,
∴CP=$\frac{9}{4}$;
②当EF=EP时,∠EPF=∠EFP,
∵∠FPB=∠BEP=90°,
∴∠FPE+∠EPB=∠B+∠EPB=90°,
∴∠B=∠FPE,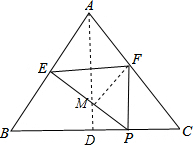
∴∠EFP=∠C,
∴△EFP∽△ABC,
设CP=x,则PF=$\frac{4}{3}$x,EP=$\frac{4}{5}$(6-x),
∴$\frac{PE}{AB}=\frac{FP}{BC}$,即$\frac{\frac{4}{5}(6-x)}{5}=\frac{\frac{4}{3}x}{6}$,
∴x=$\frac{108}{43}$,
∴CP=$\frac{108}{43}$;
③当EF=FP时,过F作FM⊥EP于M,设PC=x,
∵∠FPE+∠EPD=∠EPD+∠B=90°,
∴∠FPE=∠B=∠C,
∴△FMP∽△ADC,
∴$\frac{FP}{PM}=\frac{AC}{CD}=\frac{5}{3}$,
∴$\frac{\frac{4}{3}x}{\frac{2}{5}(6-x)}=\frac{5}{3}$,
∴x=2,
∴PC=2;
(2)①当EF∥BC时,△EFP是直角三角形,
设PC=x,则CF=$\frac{5}{3}$x,PF=$\frac{4}{3}$x,EF=$\frac{16}{9}$x,
∵$\frac{EF}{BC}=\frac{AF}{AC}$,
∴$\frac{\frac{16}{9}x}{6}$=$\frac{5-\frac{5}{3}x}{5}$,
∴x=$\frac{27}{17}$,
∴PC=$\frac{27}{17}$,
②当点F,A重合时,△EFP是直角三角形,
∵∠PPE=90°,AD=FP,
∴PC=CD=$\frac{1}{2}$BC=3.
点评 本题考查了勾股定理,等腰三角形的性质,直角三角形的性质,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
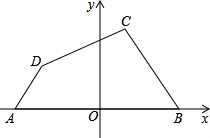 如图A(-4,0),B(6,0),C(2,4),D(-3,2).
如图A(-4,0),B(6,0),C(2,4),D(-3,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
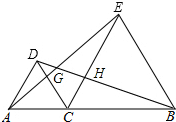 如图,△ACD,△ECB都是等边三角形,画出△ACE以点C为旋转中心,顺时针旋转60°后的三角形.若旋转后的图形的某一边与CE交于点H.求证:CG=CH.
如图,△ACD,△ECB都是等边三角形,画出△ACE以点C为旋转中心,顺时针旋转60°后的三角形.若旋转后的图形的某一边与CE交于点H.求证:CG=CH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
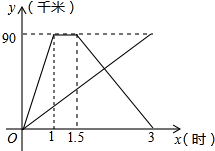 如图中,甲、乙两人同时从相距90千米的A地前往B地.甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后原路返回A地,如图是他们离A地的距离y(千米)与x(时间)之间的函数关系图象.
如图中,甲、乙两人同时从相距90千米的A地前往B地.甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后原路返回A地,如图是他们离A地的距离y(千米)与x(时间)之间的函数关系图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com