
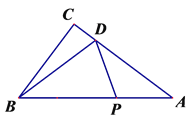
【题目】如图,在Rt△ABC中,∠C=90°AB=8cm,cos∠ABC=![]() ,点D在边AC上,且CD=
,点D在边AC上,且CD=![]() cm,动点P从点A开始沿边AB向点B以1cm/s的速度移动,当点P到达B点即停止运动.设运动时间为t(s).解答下列问题:
cm,动点P从点A开始沿边AB向点B以1cm/s的速度移动,当点P到达B点即停止运动.设运动时间为t(s).解答下列问题:
(1)M、N分别是DP、BP的中点,连接MN.
①分别求BC、MN的值;
②求在点P从点A匀速运动到点B的过程中线段MN所扫过区域的面积;
(2)在点P运动过程中,是否存在某一时刻t,使BD平分∠CDP?若存在,求出t的值;若不存在,请说明理由.

【答案】(1)①BC=![]() ;MN=
;MN=![]() ;②线段MN所扫过区域为平行四边形,面积为6
;②线段MN所扫过区域为平行四边形,面积为6![]() ;(3)
;(3) ![]()
【解析】试题分析:(1)①根据已知的AB=8和锐角三角形函数cos∠ABC=![]() ,可求出BC的长,根据勾股定理求出BD的长,然后根据三角形的中位线的性质可求解;
,可求出BC的长,根据勾股定理求出BD的长,然后根据三角形的中位线的性质可求解;
②由于D点不动,所以BD的长不变,因此MN的长不变,由此可知扫过的区域为平行四边形,然后求解即可.
(2)如图,过D作DH⊥AB于H,BE⊥PD于E,根据角平分线的性质和三角形的面积的不变性可求解.
试题解析:(1)①BC=![]() , MN=
, MN=![]() ;
;
②线段MN所扫过区域为平行四边形,
面积为6![]() ;
;
(2)存在,

如图,过D作DH⊥AB于H,BE⊥PD于E,
∵BD平分∠CDP,
∴∠PDB=∠CDB,
∴BE = BC =![]() ,
,
∴DC=DE=![]() ,
,
∵AD=AC-CD=![]() =5
=5
∴DH=3,
∵BPDH=BEPD,
∴ PD=5﹣![]() t,
t,
∴PE=![]() ﹣
﹣![]() t,
t,
∵BP2=PE2+BE2,
∴(8﹣t)2=(![]() ﹣
﹣![]() t)2+(
t)2+(![]() )2,(解此方程需要注意运算技巧,否则特别繁琐,影响运算结果与考试心情)解得:t=16(不合题意,舍去),t =
)2,(解此方程需要注意运算技巧,否则特别繁琐,影响运算结果与考试心情)解得:t=16(不合题意,舍去),t =![]() ,
,
∴当t=![]() 时,BD平分∠CDP.
时,BD平分∠CDP.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2-8ax(a<0)的图像与x轴的正半轴交于点A,它的顶点为P.点C为y轴正半轴上一点,直线AC与该图像的另一交点为B,与过点P且垂直于x轴的直线交于点D,且CB:AB=1:7.
(1)求点A的坐标及点C的坐标(用含a的代数式表示);
(2)连接BP,若△BDP与△AOC相似(点O为原点),求此二次函数的关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杭州市甲、乙两个有名的学校乐团,决定向某服装厂购买同样的演出服.如表是服装厂给出的演出服装的价格表:
购买服装的套数 | 1~39套(含39套) | 40~69套(含69套) | 70套及以上 |
每套服装的价格 | 80元 | 70元 | 60元 |
经调查:两个乐团共85人(甲乐团人数不少于46人),如果分别各自购买演出服,两个乐团共需花费6500元.请回答以下问题:
(1)如果甲、乙两个乐团联合起来购买服装,那么比各自购买服装最多可以节省多少元?
(2)甲、乙两个乐团各有多少名学生?
(3)现从甲乐团抽调a人,从乙乐团抽调b人(要求从每个乐团抽调的人数不少于5人),去儿童福利院献爱心演出,并在演出后每位乐团成员向儿童们进行“心连心活动”;甲乐团每位成员负责5位小朋友,乙乐团每位成员负责3位小朋友.这样恰好使得福利院65位小朋友全部得到“心连心活动”的温暖.请写出所有的抽调方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( ) 
A.带①去
B.带②去
C.带③去
D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于G.则下列结论中错误的是( ) 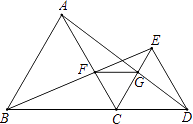
A.AD=BE
B.BE⊥AC
C.△CFG为等边三角形
D.FG∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某招聘考试分笔试和面试两种,其中笔试按60%、面试按40%计算加权平均数,作为总成绩.孔明笔试成绩90分,面试成绩85分,那么孔明的总成绩是 分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=![]() x2+bx+c与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C.
x2+bx+c与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C.
(1)求该抛物线的解析式;
(2)求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:所谓完全平方式,就是对于一个整式A,如果存在另一个整式B,使得A=B2 , 则称A是完全平方式,例如a4=(a2)2 , 4a2﹣4a+1=(2a﹣1)2 .
(1)下列各式中完全平方式的编号有①a6;②a2+ab+b2;③x2﹣4x+4y2④m2+6m+9;⑤x2﹣10x﹣25;⑥4a2+2ab+ ![]() .
.
(2)若4x2+xy+my2和x2﹣nxy+64y2都是完全平方式,求m2015n2016的值;
(3)多项式49x2+1加上一个单项式后,使它能成为一个完全平方式,那么加上的单项式可以是哪些?(请罗列出所有可能的情况,直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com