
【题目】抛物线y=![]() x2+bx+c与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C.
x2+bx+c与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C.
(1)求该抛物线的解析式;
(2)求点A关于直线y=2x的对称点A′的坐标,判定点A′是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段CA′于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(1)![]() .(2)点A/的坐标为(﹣3,4).点A/在该抛物线上.(3)点P运动到
.(2)点A/的坐标为(﹣3,4).点A/在该抛物线上.(3)点P运动到![]() 时,四边形PACM是平行四边形.
时,四边形PACM是平行四边形.
【解析】试题分析:(1)利用待定系数法求出抛物线的解析式;
(2)首先求出对称点A′的坐标,然后代入抛物线解析式,即可判定点A′是否在抛物线上.本问关键在于求出A′的坐标.如答图所示,作辅助线,构造一对相似三角形Rt△A′EA∽Rt△OAC,利用相似关系、对称性质、勾股定理,求出对称点A′的坐标;
(3)本问为存在型问题.解题要点是利用平行四边形的定义,列出代数关系式求解.如答图所示,平行四边形的对边平行且相等,因此PM=AC=10;利用含未知数的代数式表示出PM的长度,然后列方程求解.
试题解析:(1)∵![]() 与x轴交于A(5,0)、B(-1,0)两点,
与x轴交于A(5,0)、B(-1,0)两点,
∴ ,
,
解得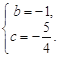
∴抛物线的解析式为![]() .
.
(2) 过点![]() 作
作![]() ⊥x轴于E,AA/与OC交于点D,
⊥x轴于E,AA/与OC交于点D,
∵点C在直线y=2x上,
∴C(5,10)
∵点A和![]() 关于直线y=2x对称,∴OC⊥
关于直线y=2x对称,∴OC⊥![]() ,
,![]() =AD.
=AD.
∵OA=5,AC=10,∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
在![]() 和
和![]() 中,
中,
∵∠![]() +∠
+∠![]() =90°,∠ACD+∠
=90°,∠ACD+∠![]() =90°,
=90°,
∴∠![]() =∠ACD.
=∠ACD.
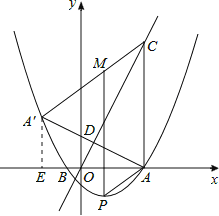
又∵∠![]() =∠OAC=90°,
=∠OAC=90°,
∴![]() ∽
∽![]() .
.
∴![]() 即
即![]() .
.
∴![]() =4,AE=8.
=4,AE=8.
∴OE=AE-OA=3.
∴点A/的坐标为(﹣3,4).
当x=﹣3时, ![]() .
.
所以,点A/在该抛物线上.
(3)存在.
理由:设直线![]() 的解析式为y=kx+b,
的解析式为y=kx+b,
则![]() ,
,
解得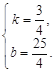
∴直线![]() 的解析式为
的解析式为![]() .
.
设点P的坐标为![]() ,则点M为
,则点M为![]() .
.
∵PM∥AC,
∴要使四边形PACM是平行四边形,只需PM=AC.又点M在点P的上方,
∴![]() .
.
解得![]() (不合题意,舍去)当x=2时,
(不合题意,舍去)当x=2时,![]() .
.
∴当点P运动到![]() 时,四边形PACM是平行四边形.
时,四边形PACM是平行四边形.


科目:初中数学 来源: 题型:
【题目】如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答. 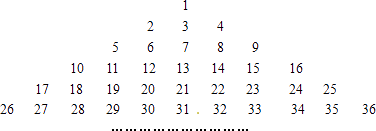
(1)表中第8行的最后一个数是 , 它是自然数的平方,第8行共有个数;
(2)用含n的代数式表示:第n行的第一个数是 , 最后一个数是 , 第n行共有个数;
(3)求第n行各数之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°AB=8cm,cos∠ABC=![]() ,点D在边AC上,且CD=
,点D在边AC上,且CD=![]() cm,动点P从点A开始沿边AB向点B以1cm/s的速度移动,当点P到达B点即停止运动.设运动时间为t(s).解答下列问题:
cm,动点P从点A开始沿边AB向点B以1cm/s的速度移动,当点P到达B点即停止运动.设运动时间为t(s).解答下列问题:
(1)M、N分别是DP、BP的中点,连接MN.
①分别求BC、MN的值;
②求在点P从点A匀速运动到点B的过程中线段MN所扫过区域的面积;
(2)在点P运动过程中,是否存在某一时刻t,使BD平分∠CDP?若存在,求出t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°. 因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
(1)求改直后的公路AB的长;
(2)问公路改直后该段路程比原来缩短了多少千米?(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校初三年级开展研究性学习,准备购买一定数量的两人学习桌和三人学习桌,如果购买3张两人学习桌,1张三人学习桌需220元;如果购买2张两人学习桌,3张三人学习桌需310元.
(1)求两人学习桌和三人学习桌的单价;
(2)学校欲投入资金不超过6000元,购买两种学习桌共98张,以至少满足248名学生的需求,设购买两人学习桌x张,购买两人学习桌和三人学习桌的总费用为W 元,求出W与x的函数关系式;求出所有的购买方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com