
 如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( )
如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( )| A. | BE⊥CE | B. | BF∥CE | C. | BE=CF | D. | AB=AC |
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:填空题
 在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点,…,则边长为8的正方形内部的整点的个数为49.
在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点,…,则边长为8的正方形内部的整点的个数为49.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
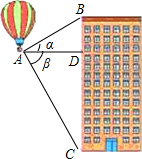 热气球的探测器显示,从热气球看一栋楼顶部的仰角α为27°,看这栋楼底部的俯角β为58°,热气球与这栋楼的水平距离为120米,这栋楼有多高(结果取整数)?
热气球的探测器显示,从热气球看一栋楼顶部的仰角α为27°,看这栋楼底部的俯角β为58°,热气球与这栋楼的水平距离为120米,这栋楼有多高(结果取整数)?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
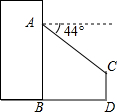 如图,李明在自家楼房的窗口A处,测量楼前的路灯CD的高度,现测得窗口处A到路灯顶部C的仰角为44°,到地面的距离AB为20米,楼底到路灯的距离BD为12米,求路灯CD的高度(结果精确到0.1)
如图,李明在自家楼房的窗口A处,测量楼前的路灯CD的高度,现测得窗口处A到路灯顶部C的仰角为44°,到地面的距离AB为20米,楼底到路灯的距离BD为12米,求路灯CD的高度(结果精确到0.1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB.
在平面直角坐标xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,二次函数y=ax2-4ax+2的图象与y轴交于点A,且过点B(3,6).
如图,二次函数y=ax2-4ax+2的图象与y轴交于点A,且过点B(3,6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com