
 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).分析 (1)画出△A1B1C1,并标出坐标;
(2)画出△A2B2C2,由旋转得:△ACO≌△A2C2O,所以线段AC扫过的部分的面积是$\frac{1}{4}$圆O的面积(半径为OA)-$\frac{1}{4}$圆O的面积(半径为OC).
解答 解:(1)如图所示A1(3,-5),B1(2,-1),C1(1,-3),
(3)如图$OA=\sqrt{{5^2}+{3^2}}=\sqrt{34}$,$OC=\sqrt{{3^2}+{1^2}}=\sqrt{10}$,
由旋转得:AO=A2O,AC=A2C2,OC=OC2,
∴△ACO≌△A2C2O,
∴线段AC扫过部分的面积为:${S_{阴影}}=\frac{1}{4}[(\sqrt{34}{)^2}-{(\sqrt{10})^2}]π=\frac{24}{4}π=6π$.
点评 本题考查了作图-旋转变换和中心对称的性质,根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形;求线段扫过的面积时,利用数形结合的方法,注意割补法组合为圆环的面积可得结果.


科目:初中数学 来源: 题型:填空题
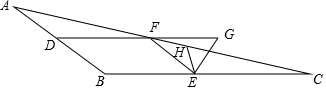 如图,已知:点D、E、F是△ABC的边AB、BC、AC上的点,DF∥BC,EF∥AB,EG平分∠FEC交DF的延长线于点G,EH平分∠BEG交AC于点H,∠EHC=40°,且∠DFE-∠C=130°,则∠B的度数为144°.
如图,已知:点D、E、F是△ABC的边AB、BC、AC上的点,DF∥BC,EF∥AB,EG平分∠FEC交DF的延长线于点G,EH平分∠BEG交AC于点H,∠EHC=40°,且∠DFE-∠C=130°,则∠B的度数为144°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com