
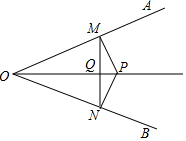
 如图,点P是∠AOB角平分线OC上任一点,若过点P分别作PM⊥OA,PN⊥OB,连接MN交OP于点Q,有如下结论:
如图,点P是∠AOB角平分线OC上任一点,若过点P分别作PM⊥OA,PN⊥OB,连接MN交OP于点Q,有如下结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 依据角平分线的性质可得到PM=PN,然后利用HL可证明Rt△OPM≌Rt△OPN,依据全等三角形的性质可证明OM=ON,最后利用等腰三角形三线合一的性质可证明③、④正确.
解答 解:∵点P是∠AOB角平分线OC上任一点,PM⊥OA,PN⊥OB,
∴PM=PN.
在Rt△OPM和Rt△OPN中$\left\{\begin{array}{l}{PM=PN}\\{OP=OP}\end{array}\right.$,
∴Rt△OPM≌Rt△OPN.
∴OM=ON.
又∵OC是∠AOB角平分线,
∴PO⊥MN,QM=QN,故③、④正确.
故选:B.
点评 本题主要考查的是全等三角形的性质和判定、角平分线的性质、等腰三角形的性质,熟练掌握相关知识是解题的关键.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:填空题
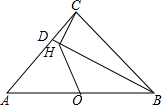 如图,△ABC中,∠ACB=90°,AC=BC=3,点D在AC上,CD=1,连接BD,过点C作CH⊥BD于点H,O为AB中点,连接OH,则OH的长为$\frac{3\sqrt{5}}{5}$.
如图,△ABC中,∠ACB=90°,AC=BC=3,点D在AC上,CD=1,连接BD,过点C作CH⊥BD于点H,O为AB中点,连接OH,则OH的长为$\frac{3\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
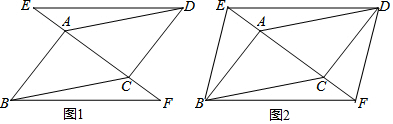
 如图所示,∠ABC=∠ACB,CD⊥AC于C,BE⊥AB于B,AE交BC于点F,且BE=CD,下列结论不一定正确的是( )
如图所示,∠ABC=∠ACB,CD⊥AC于C,BE⊥AB于B,AE交BC于点F,且BE=CD,下列结论不一定正确的是( )| A. | AB=AC | B. | BF=EF | C. | AE=AD | D. | ∠BAE=∠CAD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 职工 | 甲 | 乙 |
| 月销售件数(件) | 200 | 180 |
| 月工资(元) | 1800 | 1700 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
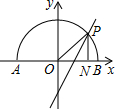 如图,半径为1的半圆的圆心在原点,直径AB在x轴上,过原点的任意一条半径与半圆交于点P,过P作PN垂直于x轴,N为垂足,则∠OPN的平分线过定点( )
如图,半径为1的半圆的圆心在原点,直径AB在x轴上,过原点的任意一条半径与半圆交于点P,过P作PN垂直于x轴,N为垂足,则∠OPN的平分线过定点( )| A. | (0,-1) | B. | (0,-$\frac{4}{5}$) | C. | (0,-$\frac{3}{5}$) | D. | (0,-$\frac{6}{5}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com