
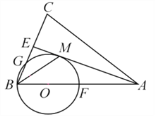
【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.
(1)求证: AE为⊙O的切线;
(2)当BC=8,AC=12时,求⊙O的半径和BG的长;
(3)在(2)的条件下,求线段BG的长.
【答案】(1)见解析;(2)r=3;(3)BG=2.
【解析】分析:(1)连接OM.利用角平分线的性质和平行线的性质得到AE⊥OM后即可证得AE是 O的切线;
(2)设 O的半径为R,根据OM∥BE,得到△OMA∽△BEA,利用平行线的性质得到![]() ,即可解得R=3,从而求得 O的半径为3;
,即可解得R=3,从而求得 O的半径为3;
(3)过点O作OH⊥BG于点H,则BG=2BH,根据∠OME=∠MEH=∠EHO=90°,得到四边形OMEH是矩形,从而得到HE=OM=3和BH=1,证得结论BG=2BH=2.
详解:(1)连接OM.∵AC=AB,AE平分∠BAC,
∴AE⊥BC,CE=BE=![]() BC,
BC,
∵OB=OM,
∴∠OBM=∠OMB,
∵BM平分∠ABC,
∴∠OBM=∠CBM,
∴∠OMB=∠CBM,
∴OM∥BC,
又∵AE⊥BC,
∴AE⊥OM,
∴AE是⊙O的切线;
(2)设⊙O的半径为r,∵OM∥BE,
∴△OMA∽△BEA,
∴![]() ,由(1)得BE=4,即
,由(1)得BE=4,即![]() ,解得r=3,
,解得r=3,
∴⊙O的半径为3;
(3)过点O作OH⊥BG于点H,
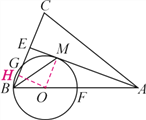
则BG=2BH,∵∠OME=∠MEH=∠EHO=90°,
∴四边形OMEH是矩形,
∴HE=OM=3,
∴BH=1,
∴BG=2BH=2.


科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:在“![]() ”中的每个□内,填入
”中的每个□内,填入![]() 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若请推算![]() □内的符号;
□内的符号;
(3)在“![]() ”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种型号汽车油箱容量为40L,每行驶100km耗油10L.设一辆加满油的该型号汽车行驶路程为x(km),行驶过程中油箱内剩余油量为y(L)
(1)求y与x之间的函数表达式;
(2)为了有效延长汽车使用寿命,厂家建议每次加油时油箱内剩余油量不低于油箱容量的四分之一,按此建议,求该辆汽车最多行驶的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准,该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.
(1)若某月用水量为18立方米,则应交水费多少元?
(2)求当x>18时,y关于x的函数表达式,若小敏家某月交水费81元,则这个月用水量为多少立方米?

查看答案和解析>>
科目:初中数学 来源: 题型:
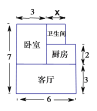
【题目】某人准备购买一套小户型住房,他去某楼盘了解情况得知,该户型单价是![]() 元/
元/![]() ,总面积如图所示(单位:米,卫生间的宽未定,设宽为
,总面积如图所示(单位:米,卫生间的宽未定,设宽为![]() 米),售房部为他提供了以下两种优惠方案: 方案一:需购买全部总面积,但整套房按原销售总金额的9折出售;
米),售房部为他提供了以下两种优惠方案: 方案一:需购买全部总面积,但整套房按原销售总金额的9折出售;
方案二:整套房的单价仍是12000元/![]() ,但不需要购买全部面积,其中,只对厨房面积进行了优惠,只算厨房
,但不需要购买全部面积,其中,只对厨房面积进行了优惠,只算厨房![]() 的面积,其余房间面积不变.
的面积,其余房间面积不变.
(1)求卫生间的面积;
(2)请分别求出两种方案购买一套该户型商品房的总金额;
(3)当1≤![]() ≤2,且
≤2,且![]() 为整数时,选哪种方案购买一套该户型商品房的总金额较少?
为整数时,选哪种方案购买一套该户型商品房的总金额较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,C都在直线l上,AE⊥AB且AE=AB,BC⊥CD且BC=CD,三点E,B,D到直线l的距离分别是6,3,4,计算图中由线段AB,BC,CD,DE,EA所围成的图形的面积是( )
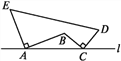
A. 50 B. 62 C. 65 D. 68
查看答案和解析>>
科目:初中数学 来源: 题型:
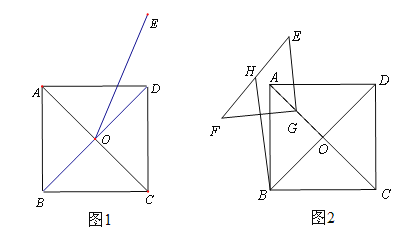
【题目】如图1,点![]() 为正方形
为正方形![]() 的中心。
的中心。
(1)将线段![]() 绕点
绕点![]() 逆时针方向旋转
逆时针方向旋转![]() ,点
,点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() ,请依题意补全图1;
,请依题意补全图1;
(2)根据图1中补全的图形,猜想并证明![]() 与
与![]() 的关系;
的关系;
(3)如图2,点![]() 是
是![]() 中点,△
中点,△![]() 是等腰直角三角形,
是等腰直角三角形, ![]() 是
是![]() 的中点,
的中点, ![]() ,
, ![]() ,
, ![]() ,△
,△![]() 绕
绕![]() 点逆时针方向旋转
点逆时针方向旋转![]() 角度,请直接写出旋转过程中
角度,请直接写出旋转过程中![]() 的最大值。
的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0)
⑴画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
⑵画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O;
⑶在x轴上存在一点P,满足点P到A1与点A2距离之和最小,请直接写出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s.连结PO并延长交BC于点Q,设运动时间为t(0<t<5).
(1)当t为何值时,四边形ABQP是平行四边形?
(2)设四边形OQCD的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使点O在线段AP的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.

 备用图
备用图
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com