
【题目】某人准备购买一套小户型住房,他去某楼盘了解情况得知,该户型单价是![]() 元/
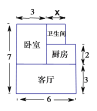
元/![]() ,总面积如图所示(单位:米,卫生间的宽未定,设宽为
,总面积如图所示(单位:米,卫生间的宽未定,设宽为![]() 米),售房部为他提供了以下两种优惠方案: 方案一:需购买全部总面积,但整套房按原销售总金额的9折出售;
米),售房部为他提供了以下两种优惠方案: 方案一:需购买全部总面积,但整套房按原销售总金额的9折出售;
方案二:整套房的单价仍是12000元/![]() ,但不需要购买全部面积,其中,只对厨房面积进行了优惠,只算厨房
,但不需要购买全部面积,其中,只对厨房面积进行了优惠,只算厨房![]() 的面积,其余房间面积不变.
的面积,其余房间面积不变.
(1)求卫生间的面积;
(2)请分别求出两种方案购买一套该户型商品房的总金额;
(3)当1≤![]() ≤2,且
≤2,且![]() 为整数时,选哪种方案购买一套该户型商品房的总金额较少?
为整数时,选哪种方案购买一套该户型商品房的总金额较少?
【答案】(1)2x;(2)方案一:![]() ,方案二:
,方案二:![]() ;(3)当
;(3)当![]() =1时,选择方案二所需金额较少;当
=1时,选择方案二所需金额较少;当![]() =2时,选择方案一和方案二所需金额一样.
=2时,选择方案一和方案二所需金额一样.
【解析】
(1)根据题意列出代数式即可解答;
(2)根据题意分别求出两个方案所需的金额即可;
(3)把1≤![]() ≤2,且
≤2,且![]() 为整数时,分别代入两个方案的代数式里面进行解答即可.
为整数时,分别代入两个方案的代数式里面进行解答即可.
解:(1)卫生间的面积是:(7-3-2)![]() =2
=2![]()
(2)方案一所需总金额为:![]()
![]()
![]() .
.
方案二所需总金额为:![]()
![]()
![]() .
.
(3)当![]() =1时,方案一所需总金额410400元,方案二所需总金额408000元,
=1时,方案一所需总金额410400元,方案二所需总金额408000元,
∵410400>408000
∴选择方案二所需金额较少;
当![]() =2时,方案一所需总金额432000元,方案二所需总金额432000元,
=2时,方案一所需总金额432000元,方案二所需总金额432000元,
∵432000=432000
∴选择方案一和方案二所需金额一样.


科目:初中数学 来源: 题型:
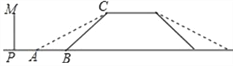
【题目】某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:![]() .
.
(1)求新坡面的坡角∠CAB的度数;
(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1), 已知△ABC中, ∠BAC=900, AB=AC, AE是过A的一条直线, 且B.C在A.E的异侧, BD⊥AE于D, CE⊥AE于E
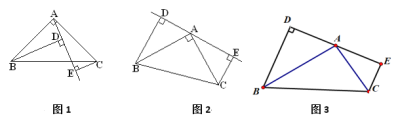
(1)试说明: BD=DE+CE.
(2)若直线AE绕A点旋转到图(2)位置时, 其余条件不变, 问BD与DE.CE的数量关系如何?请直接写出结果, 不需说明
(3)如图(3)若将图(2)中的AB=AC改为∠ABD=∠ABC其余条件不变, 问AD与AE的数量关系如何? 并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备进一批小工艺品,每件的成本是40元,经市场调查,销售单价为50元,每天销售量为100个,若销售单价每增加1元,销售量将减少10个.
(1)求每天销售小工艺品的利润y(元)和销售单价x(元)之间的函数解析式;
(2)商店若准备每天销售小工艺品获利960元,则每天销售多少个?销售单价定为多少元?
(3)直接写出销售单价为多少元时,每天销售小工艺品的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
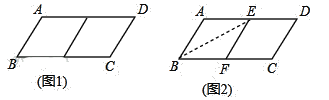
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下的一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.
(1)猜想与计算:
邻边长分别为3和5的平行四边形是_______阶准菱形;已知ABCD的邻边长分别为a,b(a>b),满足a=8b+r,b=5r,请写出ABCD___________阶准菱形.
(2)操作与推理:
小明为了剪去一个菱形,进行了如下操作:如图2,把ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.请证明四边形ABFE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
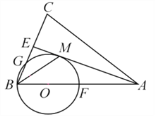
【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.
(1)求证: AE为⊙O的切线;
(2)当BC=8,AC=12时,求⊙O的半径和BG的长;
(3)在(2)的条件下,求线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的正偶数2,4,6,8…,排成下表:
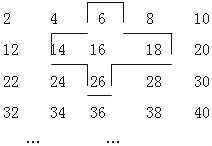
(1)十字框中的五个数的和是中间的数16的几倍?
(2)若将十字框上下左右移动,可框住另外的五个数,设中间的数为![]() ,用代数式表示十字框中的五个数的和;
,用代数式表示十字框中的五个数的和;
(3)这五个数的和能等于2010吗?如能,写出这五个数,如不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,图(1)中含“○”的矩形有1个,图(2)中含“○”的矩形有7个,图(3)中含“○”的矩形有17个,按此规律,图(6)中含“○”的矩形有( )
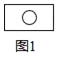
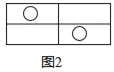
A. 70 B. 71 C. 72 D. 73
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,∠ABC=60°,AB=4,AD=8,点E,F分别是边BC,AD的中点,点M是AE与BF的交点,点N是CF与DE的交点,则四边形ENFM的周长是______.
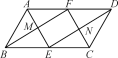
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com