
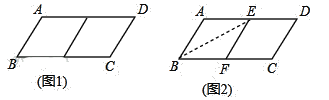
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下的一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.
(1)猜想与计算:
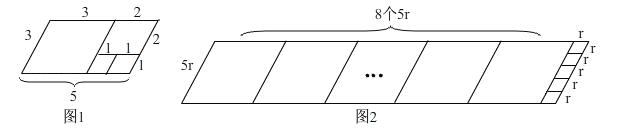
邻边长分别为3和5的平行四边形是_______阶准菱形;已知ABCD的邻边长分别为a,b(a>b),满足a=8b+r,b=5r,请写出ABCD___________阶准菱形.
(2)操作与推理:
小明为了剪去一个菱形,进行了如下操作:如图2,把ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.请证明四边形ABFE是菱形.
【答案】(1)3,12;(2)证明见解析.
【解析】试题分析:(1)利用平行四边形准菱形的意义即可得出结论;
(2)先判断出∠AEB=∠ABE,进而判断出AE=BF,即可得出结论.
试题解析:解:(1)如图1,利用邻边长分别为3和5的平行四边形进行3次操作,所剩四边形是边长为1的菱形,故邻边长分别为3和5的平行四边形是3阶准菱形:
如图2,∵b=5r,∴a=8b+r=40r+r=8×5r+r,利用邻边长分别为41r和5r的平行四边形进行8+4=12次操作,所剩四边形是边长为1的菱形,故邻边长分别为41r和5r的平行四边形是12阶准菱形:
故答案为:3,12.
(2)由折叠知:∠ABE=∠FBE,AB=BF,∵四边形ABCD是平行四边形,∴AE∥BF,∴∠AEB=∠FBE,∴∠AEB=∠ABE,∴AE=AB,∴AE=BF,∴四边形ABFE是平行四边形,∴四边形ABFE是菱形.


科目:初中数学 来源: 题型:
【题目】下面表格给出了直线![]() 上部分点(x,y)的坐标值.
上部分点(x,y)的坐标值.
x | -2 | 0 | 2 | 4 |
y | 3 | 1 | -1 | -3 |
(1)直线![]() 与
与![]() 轴的交点坐标是___________;
轴的交点坐标是___________;
(2)直线![]() 与两坐标轴围成的三角形的面积等于___________.
与两坐标轴围成的三角形的面积等于___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
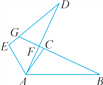
【题目】如图,△ABC≌△ADE,已知点C和点E是对应点,BC的延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°,试求∠DFB和∠DGB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国梦”关系每个人的幸福生活,为展现广安人追梦的风采,我市某中学举行“中国梦我的梦”的演讲比赛,赛后整理参赛学生的成绩,将学的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整,请你根据统计图解答下列问题.
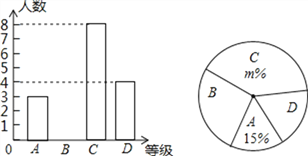
(1)补全条形统计图;
(2)组委会决定从本次比赛中获得A等级的学生中,选出2名去参加市中学生演讲比赛,已知A等级中男生有1名,请用“列表”或“画树状图”的方法求出所选2名学生中恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
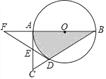
【题目】如图,在Rt△ABC中,∠BAC=90°,以AB为直径作⊙O交BC于点D,E为AC的中点,连接DE并延长交BA的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若∠F=30°,⊙O的半径为2![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
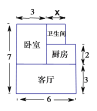
【题目】某人准备购买一套小户型住房,他去某楼盘了解情况得知,该户型单价是![]() 元/
元/![]() ,总面积如图所示(单位:米,卫生间的宽未定,设宽为
,总面积如图所示(单位:米,卫生间的宽未定,设宽为![]() 米),售房部为他提供了以下两种优惠方案: 方案一:需购买全部总面积,但整套房按原销售总金额的9折出售;
米),售房部为他提供了以下两种优惠方案: 方案一:需购买全部总面积,但整套房按原销售总金额的9折出售;
方案二:整套房的单价仍是12000元/![]() ,但不需要购买全部面积,其中,只对厨房面积进行了优惠,只算厨房
,但不需要购买全部面积,其中,只对厨房面积进行了优惠,只算厨房![]() 的面积,其余房间面积不变.
的面积,其余房间面积不变.
(1)求卫生间的面积;
(2)请分别求出两种方案购买一套该户型商品房的总金额;
(3)当1≤![]() ≤2,且
≤2,且![]() 为整数时,选哪种方案购买一套该户型商品房的总金额较少?
为整数时,选哪种方案购买一套该户型商品房的总金额较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应环保组织提出的“低碳生活”的号召,李明决定不开汽车而改骑自行车上班.有一天,李明骑自行车从家里到工厂上班,途中因自行车发生故障,修车耽误了一段时间,车修好后继续骑行,直至到达工厂(假设在骑自行车过程中匀速行驶).李明离家的距离![]() (米)与离家时间
(米)与离家时间![]() (分钟)的关系表示如下图:
(分钟)的关系表示如下图:
(1)李明从家出发到出现故障时的速度为 米/分钟;
(2)李明修车用时 分钟;
(3)求线段BC所对应的函数关系式(不要求写出自变量的取值范围).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②∠DFB=![]() ∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的结论是_______.
∠CGE;③∠ADC=∠GCD;④CA平分∠BCG.其中正确的结论是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
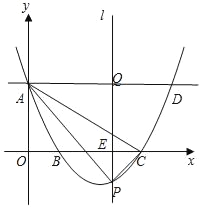
【题目】如图,在平面直角坐标系中,抛物线y=mx2﹣7mx+3与y轴交于点A,与x轴分别交于点B(1,0).点C(x2,0),过点A作直线AD∥x轴,与抛物线交于点D,在x轴上有一动点E(t,0),过点E作直线l∥y轴,与抛物线交于点P,与直线AD交于点Q.
(1)求抛物线的解析式及点C的坐标;
(2)当0<t≤7时,求△APC面积的最大值;
(3)当t>1时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似?若存在,求出此时t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com