
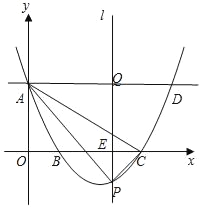
【题目】如图,在平面直角坐标系中,抛物线y=mx2﹣7mx+3与y轴交于点A,与x轴分别交于点B(1,0).点C(x2,0),过点A作直线AD∥x轴,与抛物线交于点D,在x轴上有一动点E(t,0),过点E作直线l∥y轴,与抛物线交于点P,与直线AD交于点Q.
(1)求抛物线的解析式及点C的坐标;
(2)当0<t≤7时,求△APC面积的最大值;
(3)当t>1时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似?若存在,求出此时t的值;若不存在,请说明理由.
【答案】(1)当x=1时,m﹣7m+3=1;(2)当t=7时,S△APC最大=![]() ,当t=3时,S△APC最大=
,当t=3时,S△APC最大=![]() ;
;
(3)存在,t=![]() 或
或![]() 或13.
或13.
【解析】分析:
(1)先将点B坐标代入抛物线解析式求出m,即可得出结论;
(2)分两种情况,利用面积和或差得出函数关系式,即可得出结论;
(3)分两种情况,利用相似三角形的性质得出比例式建立方程求解即可得出结论.
详解:(1)当x=1时,m﹣7m+3=1;
∴m=![]() ,
,
∴抛物线解析式为y=![]() x2﹣
x2﹣![]() x+3,
x+3,
当y=0时,0=![]() x2﹣
x2﹣![]() x+3,
x+3,
∴x=1或x=6,
∴C(6,0);
(2)由题意知,点P与点C不能重合,
∴t≠6,
∵A(0,3),C(6,0),
∴直线AC的解析式为y=﹣![]() +3,
+3,
∵E(t,0),
设直线AC与l的交点为F,
∴F(t,﹣![]() t+3),
t+3),
当0<t<6时,FP=﹣![]() t2+3t,
t2+3t,
∴S△APC=S△APF+S△PFC=﹣![]() (t﹣3)2+
(t﹣3)2+![]() ,
,
当t=3时,S△APC最大=![]() ,
,
当6<t≤7时,S△APC=S△APF﹣S△PFC=![]() (t﹣3)2﹣
(t﹣3)2﹣![]() ,
,
当t=7时,S△APC最大=![]() ,
,
∴当t=3时,S△APC最大=![]() ;
;
(3)存在,
理由:在△AOB中,OA=3,OB=1,∠AOB=90°,P(t,![]() t2﹣
t2﹣![]() t+3),
t+3),
∵点P和点D不能重合,
∴t≠7,
当1<t<7时,QA=t,QP=﹣![]() t2+
t2+![]() t,
t,
若△AOB与△AQP相似,
∴![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
∴t1=0(舍),t2=![]() 或t3=0(舍),t4=1(舍)
或t3=0(舍),t4=1(舍)
当t>7时,QA=t,PQ=![]() t2﹣
t2﹣![]() t,
t,
若△AOP与△AOB相似,
∴![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
∴t5=0(舍)或t=![]() 或t7=0(舍)t8=13,
或t7=0(舍)t8=13,
综上述,t=![]() 或
或![]() 或13.
或13.


科目:初中数学 来源: 题型:
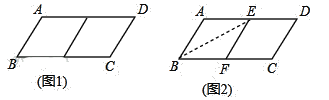
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下的一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.
(1)猜想与计算:
邻边长分别为3和5的平行四边形是_______阶准菱形;已知ABCD的邻边长分别为a,b(a>b),满足a=8b+r,b=5r,请写出ABCD___________阶准菱形.
(2)操作与推理:
小明为了剪去一个菱形,进行了如下操作:如图2,把ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.请证明四边形ABFE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数y=2x2﹣mx+m﹣2,以下结论:
①抛物线交x轴有交点;
②不论m取何值,抛物线总经过点(1,0);
③若m>6,抛物线交x轴于A、B两点,则AB>1;
④抛物线的顶点在y=﹣2(x﹣1)2图象上.其中正确的序号是( )
A. ①②③④ B. ①②③ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材母题 点P(x,y)在第一象限,且x+y=8,点A的坐标为(6,0).设△OPA的面积为S.
(1)用含有x的式子表示S,写出x的取值范围,画出函数S的图象;
(2)当点P的横坐标为5时,△OPA的面积为多少?
(3)△OPA的面积能大于24吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民用电的电价实行阶梯收费,收费标准如下表:
一户居民每月用电量x(度) | 电费价格(元/度) |
| 0.48 |
| 0.53 |
| 0.78 |
七月份是用电高峰期,李叔计划七月份电费支出不超过200元,则李叔家七月份最多可用电的度数是( ).
A. 100B. 400C. 396D. 397
查看答案和解析>>
科目:初中数学 来源: 题型:
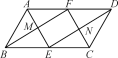
【题目】如图,ABCD中,∠ABC=60°,AB=4,AD=8,点E,F分别是边BC,AD的中点,点M是AE与BF的交点,点N是CF与DE的交点,则四边形ENFM的周长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
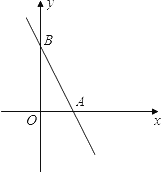
【题目】如图,直线![]() 与
与![]() 轴相交于点A,与
轴相交于点A,与![]() 轴相交于点B.
轴相交于点B.
(1)求A、B两点的坐标;
(2)求△AOB的面积;
(3)若点P是![]() 轴上的一个动点,且△PAB是等腰三角形,则P点的坐标为___________.
轴上的一个动点,且△PAB是等腰三角形,则P点的坐标为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com