练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某市居民用电的电价实行阶梯收费，收费标准如下表:

    一户居民每月用电量x(度)

    电费价格(元/度)

    0.48

    0.53

    0.78

    七月份是用电高峰期，李叔计划七月份电费支出不超过200元，则李叔家七月份最多可用电的度数是( ).

    A. 100B. 400C. 396D. 397

    【答案】C

    【解析】

    先判断出电费是否超过400度，然后根据不等关系：七月份电费支出不超过200元，列不等式计算即可．

    解：0.48×200+0.53×200
    =96+106
    =202（元），
    故七月份电费支出不超过200元时电费不超过400度，
    依题意有0.48×200+0.53（x-200）≤200，
    解得x≤396．
    答：李叔家七月份最多可用电的度数是396．
    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

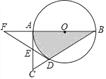
    【题目】如图，在Rt△ABC中，∠BAC=90°，以AB为直径作⊙O交BC于点D，E为AC的中点，连接DE并延长交BA的延长线于点F．

    （1）求证：DE是⊙O的切线；

    （2）若∠F=30°，⊙O的半径为2，求图中阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，反比例函数y=的图象上，点A是该图象第一象限分支上的动点，连结AO并延长交另一支于点B，以AB为斜边作等腰直角△ABC，顶点C在第四象限，AC与x轴交于点P，连结BP，在点A运动过程中，当BP平分∠ABC时，点A的坐标为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，将坐标原点O沿x轴向左平移2个单位长度得到点A，过点A作y轴的平行线交反比例函数y=的图象于点B，AB=．

    （1）求反比例函数的解析式；

    （2）若P（x1，y1）、Q（x2，y2）是该反比例函数图象上的两点，且x1＜x2时，y1＞y2，指出点P、Q各位于哪个象限？并简要说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=k1x+b（k1≠0）与双曲线（k2≠0）相交于A（1，2）、B（m，﹣1）两点．

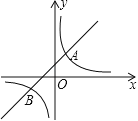
    （1）求直线和双曲线的解析式；

    （2）若A1（x1，y1），A2（x2，y2），A3（x3，y3）为双曲线上的三点，且x1＜0＜x2＜x3，请直接写出y1，y2，y3的大小关系式；

    （3）观察图象，请直接写出不等式k1x+b＜的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

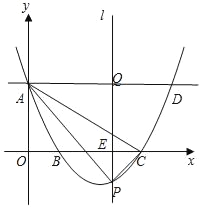
    【题目】如图，在平面直角坐标系中，抛物线y=mx2﹣7mx+3与y轴交于点A，与x轴分别交于点B（1，0）．点C（x2，0），过点A作直线AD∥x轴，与抛物线交于点D，在x轴上有一动点E（t，0），过点E作直线l∥y轴，与抛物线交于点P，与直线AD交于点Q．

    （1）求抛物线的解析式及点C的坐标；

    （2）当0＜t≤7时，求△APC面积的最大值；

    （3）当t＞1时，是否存在点P，使以A、P、Q为顶点的三角形与△AOB相似？若存在，求出此时t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

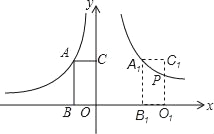
    【题目】如图，在平面直角坐标系中，矩形ABOC的两边在坐标轴上，OB=1，点A在函数y=﹣（x＜0）的图象上，将此矩形向右平移3个单位长度到A1B1O1C1的位置，此时点A1在函数y=（x＞0）的图象上，C1O1与此图象交于点P，则点P的纵坐标是（　　）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

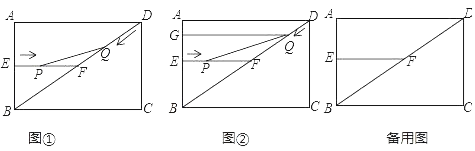
    【题目】如图1，在矩形ABCD中，AB=6cm，BC=8cm，E、F分别是AB、BD的中点，连接EF，点P从点E出发，沿EF方向匀速运动，速度为1cm/s，同时，点Q从点D出发，沿DB方向匀速运动，速度为2cm/s，当点P停止运动时，点Q也停止运动．连接PQ，设运动时间为t（0＜t＜4）s，解答下列问题：

    （1）求证：△BEF∽△DCB；

    （2）当点Q在线段DF上运动时，若△PQF的面积为0.6cm2，求t的值；

    （3）如图2过点Q作QG⊥AB，垂足为G，当t为何值时，四边形EPQG为矩形，请说明理由；

    （4）当t为何值时，△PQF为等腰三角形？试说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，⊙O的半径为r（r＞0），若点P′在射线OP上，满足OP′OP=r2，则称点P′是点P关于⊙O的“反演点”．

    如图2，⊙O的半径为4，点B在⊙O上，∠BOA=60°，OA=8，若点A′，B′分别是点A，B关于⊙O的反演点，求A′B′的长．

    查看答案和解析>>

    同步练习册答案