
【题目】如图,在Rt△ABC中,∠BAC=90°,以AB为直径作⊙O交BC于点D,E为AC的中点,连接DE并延长交BA的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若∠F=30°,⊙O的半径为2![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
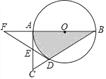
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1) 连接OD、AD,利用直径所对圆周角是直角,可求得△ADC是直角三角形,利用半径构成的等腰三角形找等角,可得∠ODE=90°.(2)求出直角三角形和扇形的面积求和.
试题解析:
解:(1)如图,连接OD、AD,
∵AB为⊙O的直径,
∴△ADC是直角三角形,
∵E为AC的中点,
∴AE=EC=DE,
∴∠ADE=∠DAE,
∵OA=OD,
∴∠OAD=∠ODA,
∵∠BAC=90°,
∴∠OAD+∠DAE=90°,
∴∠ODA+∠ADE=90°,
即∠ODE=90°,OD⊥DE,
∴DE是⊙O的切线;
(2)∵∠F=30° OD⊥DE,
∴∠AOD=60°
又∵r=2![]() .
.
∴图中阴影部分面积=![]() AD
AD![]() =
=![]() .
.


科目:初中数学 来源: 题型:
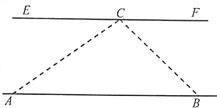
【题目】如图,湛河两岸AB与EF平行,小亮同学假期在湛河边A点处,测得对岸河边C处视线与湛河岸的夹角∠CAB=37°,沿河岸前行140米到点B处,测得对岸C处的视线与湛河岸夹角∠CBA=45°.问湛河的宽度约多少米?(参考数据:sin37°≈0.60,cos37°=0.80,tan37°=0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明购买了一套安居型商品房,他准备将地面铺上地砖,地面结构如图所示.请根据图中的数据(单位:m),解答下列问题:
(1)用含x、y的代数式表示地面总面积;
(2)若x=5,y=![]() ,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?
,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
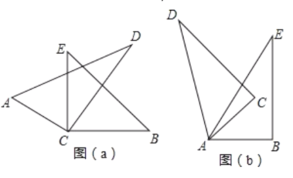
【题目】(1)如图(a),将一副三角尺(∠A=60°,∠B=45°)的直角顶点C叠放在一起,边CD与BE相交.
①若∠DCE=25°,则∠ACB=_____;若∠ACB=130°,则∠DCE= _____ ;
②猜想∠ACB与∠DCE的数量关系.直接写出答案,无需证明.
(2)如图(b),若两个相同的三角尺60°锐角的顶点A重合在一起, 边CD与A E相交,则∠DAB与∠CAE有何数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)
![]()
(1)数轴上点B对应的数是______.
(2)经过几秒,点M、点N分别到原点O的距离相等?
(3)当点M运动到什么位置时,恰好使AM=2BN?
查看答案和解析>>
科目:初中数学 来源: 题型:
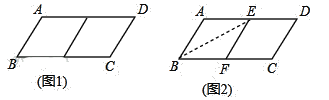
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下的一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.
(1)猜想与计算:
邻边长分别为3和5的平行四边形是_______阶准菱形;已知ABCD的邻边长分别为a,b(a>b),满足a=8b+r,b=5r,请写出ABCD___________阶准菱形.
(2)操作与推理:
小明为了剪去一个菱形,进行了如下操作:如图2,把ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.请证明四边形ABFE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
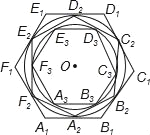
【题目】如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A11B11C11D11E11F11的边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民用电的电价实行阶梯收费,收费标准如下表:
一户居民每月用电量x(度) | 电费价格(元/度) |
| 0.48 |
| 0.53 |
| 0.78 |
七月份是用电高峰期,李叔计划七月份电费支出不超过200元,则李叔家七月份最多可用电的度数是( ).
A. 100B. 400C. 396D. 397
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com