
【题目】(1)如图(a),将一副三角尺(∠A=60°,∠B=45°)的直角顶点C叠放在一起,边CD与BE相交.
①若∠DCE=25°,则∠ACB=_____;若∠ACB=130°,则∠DCE= _____ ;
②猜想∠ACB与∠DCE的数量关系.直接写出答案,无需证明.
(2)如图(b),若两个相同的三角尺60°锐角的顶点A重合在一起, 边CD与A E相交,则∠DAB与∠CAE有何数量关系?请说明理由.
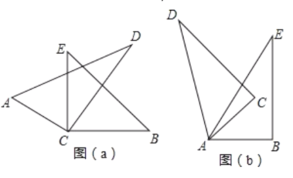
【答案】(1)①155°,50°,②∠ACB+∠DCE=180°;(2)∠DAB+∠CAE=120°,理由见解析
【解析】
(1)①先求出∠BCD,再代入∠ACB=∠ACD+∠BCD求出即可;先求出∠BCD,再代入∠DCE=∠BCE∠BCD求出即可;②根据∠ACB=∠ACE+∠DCE+∠DCE求出即可;
(2)根据∠DAB=∠DAE+∠CAE+∠CAB求出即可;
(1)①∵∠BCE=90°,∠DCE=25°,
∴∠BCD=∠BCE∠DCE=65°,
∵∠ACD=90°,
∴∠ACB=∠ACD+∠BCD=90°+65°=155°;
∵∠ACB=130°,∠ACD=90°,
∴∠BCD=∠ACB∠ACD=130°90°=40°,
∵∠BCE=90°,
∴∠DCE=∠BCE∠BCD=90°40°=50°,
故答案为:155°,50°;
②∠ACB+∠DCE=180°,
理由如下:∵∠ACB=∠ACE+∠DCE+∠DCE,
∴∠ACB+∠DCE
=∠ACE+∠DCE+∠DCE+∠DCE
=∠ACD+∠BCE
=180°;
(2)∠DAB+∠CAE=120°,理由如下:
∵∠DAB=∠DAE+∠CAE+∠CAB,
∴∠DAB+∠CAE
=∠DAE+∠CAE+∠CAB+∠CAE
=∠DAC+∠BAE
=120°.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】如图O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)求∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx(a≠0)的图象过原点O和点A(1, ![]() ),且与x轴交于点B,△AOB的面积为
),且与x轴交于点B,△AOB的面积为![]() 。
。
(1)求抛物线的解析式;
(2)若抛物线的对称轴上存在一点M,使△AOM的周长最小,求M点的坐标;
(3)点F是x轴上一动点,过F作x轴的垂线,交直线AB于点E,交抛物线于点P,且PE=![]() ,直接写出点E的坐标(写出符合条件的两个点即可)。
,直接写出点E的坐标(写出符合条件的两个点即可)。


查看答案和解析>>
科目:初中数学 来源: 题型:
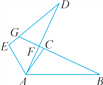
【题目】如图,△ABC≌△ADE,已知点C和点E是对应点,BC的延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°,试求∠DFB和∠DGB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求证:等腰三角形底边中线上任意一点到两腰的距离相等.
(1)在所给图形的基础上,根据题意画出图形.
(2)根据所画图形写出已知、求证.
(3)写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国梦”关系每个人的幸福生活,为展现广安人追梦的风采,我市某中学举行“中国梦我的梦”的演讲比赛,赛后整理参赛学生的成绩,将学的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整,请你根据统计图解答下列问题.
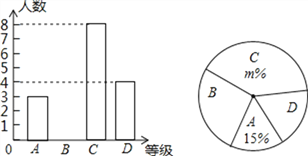
(1)补全条形统计图;
(2)组委会决定从本次比赛中获得A等级的学生中,选出2名去参加市中学生演讲比赛,已知A等级中男生有1名,请用“列表”或“画树状图”的方法求出所选2名学生中恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
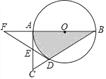
【题目】如图,在Rt△ABC中,∠BAC=90°,以AB为直径作⊙O交BC于点D,E为AC的中点,连接DE并延长交BA的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若∠F=30°,⊙O的半径为2![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应环保组织提出的“低碳生活”的号召,李明决定不开汽车而改骑自行车上班.有一天,李明骑自行车从家里到工厂上班,途中因自行车发生故障,修车耽误了一段时间,车修好后继续骑行,直至到达工厂(假设在骑自行车过程中匀速行驶).李明离家的距离![]() (米)与离家时间
(米)与离家时间![]() (分钟)的关系表示如下图:
(分钟)的关系表示如下图:
(1)李明从家出发到出现故障时的速度为 米/分钟;
(2)李明修车用时 分钟;
(3)求线段BC所对应的函数关系式(不要求写出自变量的取值范围).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数y=![]() 的图象于点B,AB=
的图象于点B,AB=![]() .
.
(1)求反比例函数的解析式;
(2)若P(x1,y1)、Q(x2,y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2,指出点P、Q各位于哪个象限?并简要说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com