
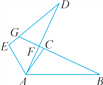
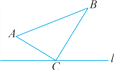
【题目】如图,△ABC≌△ADE,已知点C和点E是对应点,BC的延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°,试求∠DFB和∠DGB的度数.
【答案】90°;65°
【解析】试题分析:根据全等三角形的性质可得∠BAC=∠DAE,根据三角形的内角和定理求出∠BAC,再求出∠BAD,然后根据三角形的一个外角等于与它不相邻的两个内角的和分别求解即可.
试题解析:
∵△ABC≌△ADE,∴∠BAC=∠DAE.
∵∠EAB=∠BAC+∠DAC+∠DAE,∠DAC=10°,∠EAB=120°,
∴∠BAC=∠DAE=55°.
∴∠BAD=∠CAD+∠BAC=65°.
∵∠DFB是△ABF的一个外角,
∴∠DFB=∠BAF+∠B=65°+25°=90°.
又∵∠DFB是△DFG的一个外角,
∴∠DFB=∠D+∠DGB,
∴∠DGB=∠DFB-∠D=90°-25°=65°.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案科目:初中数学 来源: 题型:
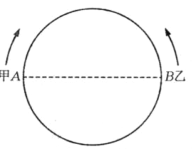
【题目】某校为培养青少年科技创新能力,举办了动漫制作活动,小明设计了点做圆周运动的一个雏型.如图所示,甲、乙两点分别从直径的两端点 A、B以顺时针、逆时针的方向同时沿圆周运动. 甲运动的路程l(cm)与时间t(s)满足关系:![]() (t≥0),乙以4 cm/s的速度匀速运动,半圆的长度为 21 cm.
(t≥0),乙以4 cm/s的速度匀速运动,半圆的长度为 21 cm.
(1)甲运动 4 s后的路程是多少?
(2)甲、乙从开始运动到第一次相遇时,它们运动了多少时间?
(3)甲、乙从开始运动到第二次相遇时,它们运动了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)交x轴于A(﹣1,0),B(5,0)两点,与y轴交于点C(0,2)
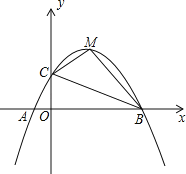
(1)求抛物线的解析式;
(2)若点M为抛物线的顶点,连接BC、CM、BM,求△BCM的面积;
(3)连接AC,在x轴上是否存在点P使△ACP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
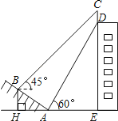
【题目】如图,某大楼的顶部树有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度![]() ,AB=10米,AE=15米.
,AB=10米,AE=15米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“故人西辞黄鹤楼,烟花三月下扬州”,据报道去年扬州旅游总收入近900亿元,大部分的旅游收入是靠“皮包骨“的湖泊﹣﹣瘦西湖得来.将数据90000000000用科学记数法表示为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=6,BC=8.点P从点A出发沿路径A→C→B向终点B运动;点Q从点B出发沿路径B→C→A向终点A运动.点P和点Q分别以1个单位/秒和3个单位/秒的速度同时开始运动,两点都要到相应的终点时才能停止运动,在某一时刻,过点P作PE⊥l于点E,过点Q作QF⊥l于点F.问:点P运动多少时间时,△PEC与△CFQ全等?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级(2)班派出12名同学参加数学竞赛,老师以75分为基准,把分数超过75分的部分记为正数,不足的部分记为负数.评分记录如下:
+15,+20,-5,-4,-3,+4,+6,+2,+3,+5,+7,-8
(1)这12名同学中最高分和最低分各是多少分?
(2)超过基准分的有多少人?
(3)这12名同学的平均成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备食建一个面积为200m2的矩形花圃,它的长比宽多10m,设花圃的宽为x m.则可列方程为( )
A.x (x﹣10)=200
B.2x+2 (x﹣10)=200
C.x(x+10)=200
D.2x+2(x+10)=200
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com