
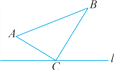
【题目】如图,在△ABC中,∠ACB=90°,AC=6,BC=8.点P从点A出发沿路径A→C→B向终点B运动;点Q从点B出发沿路径B→C→A向终点A运动.点P和点Q分别以1个单位/秒和3个单位/秒的速度同时开始运动,两点都要到相应的终点时才能停止运动,在某一时刻,过点P作PE⊥l于点E,过点Q作QF⊥l于点F.问:点P运动多少时间时,△PEC与△CFQ全等?请说明理由.
【答案】见解析
【解析】试题分析:由全等三角形的对应边相等可得CP=CQ,分①P在AC上,Q在BC上,②P、Q都在AC上,③当Q到A点,与A重合,P在BC上时3种情况求解即可.
试题解析:
解:设运动时间为t(s)时,△PEC≌△CFQ.
∵△PEC≌△CFQ,∴斜边CP=QC.
当0<t<6时,点P在AC上;
当6≤t≤14时,点P在BC上.
当0<t<![]() 时,点Q在BC上;
时,点Q在BC上;
当![]() 时,点Q在AC上.
时,点Q在AC上.
有三种情况:①当点P在AC上,点Q在BC上时![]() ,如解图①.
,如解图①.
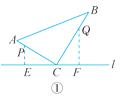
易得CP=6-t,QC=8-3t,
∴6-t=8-3t,解得t=1.
②当点P,Q都在AC上时![]() ,此时点P,Q重合,如解图②.
,此时点P,Q重合,如解图②.
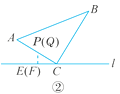
易得CP=6-t=3t-8,解得t=3.5.
③当点Q与点A重合,点P在BC上时(6<t≤14),如解图③.
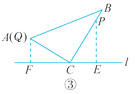
易得CP=t-6,QC=6,∴t-6=6,解得t=12.
综上所述,当点P运动1 s或3.5 s或12 s时,△PEC与△CFQ全等.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
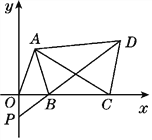
【题目】如图,在平面直角坐标系中,已知点A(a-1,a+b),B(a,0),且(a+b-3)2+|a-2b|=0,C为x轴上点B右侧的动点,以AC为腰作等腰三角形ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.
(1)线段AO与线段AB的数量关系是______(填“>”、“≥”、“≤”、“<”或“=”);
(2)求证:△AOC≌△ABD;
(3)若∠CAD=30![]() ,当点C运动时,点P在y轴上的位置是否发生改变,为什么?
,当点C运动时,点P在y轴上的位置是否发生改变,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D。

(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
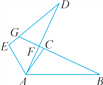
【题目】如图,△ABC≌△ADE,已知点C和点E是对应点,BC的延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°,试求∠DFB和∠DGB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
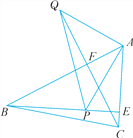
【题目】如图,已知在△ABC中,AB>AC,BE,CF都是△ABC的高线,P是BE上一点,且BP=AC,Q是CF延长线上一点,且CQ=AB,连结AP,AQ,QP.求证:
(1)AQ=PA.
(2)AP⊥AQ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com