
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЕуA(aЃ1ЃЌaЃЋb)ЃЌB(aЃЌ0)ЃЌЧв(aЃЋbЃ3)2ЃЋ|aЃ2b|=0ЃЌCЮЊxжсЩЯЕуBгвВрЕФЖЏЕуЃЌвдACЮЊбќзїЕШбќШ§НЧаЮACDЃЌЪЙAD=ACЃЌЁЯCAD=ЁЯOABЃЌжБЯпDBНЛyжсгкЕуP.
ЃЈ1ЃЉЯпЖЮAOгыЯпЖЮABЕФЪ§СПЙиЯЕЪЧ______ЃЈЬюЁА>ЁБЁЂЁАЁнЁБЁЂЁАЁмЁБЁЂЁА<ЁБЛђЁА=ЁБЃЉЃЛ
ЃЈ2ЃЉЧѓжЄЃКЁїAOCЁеЁїABDЃЛ
ЃЈ3ЃЉШєЁЯCAD=30![]() ЃЌЕБЕуCдЫЖЏЪБЃЌЕуPдкyжсЩЯЕФЮЛжУЪЧЗёЗЂЩњИФБфЃЌЮЊЪВУДЃП
ЃЌЕБЕуCдЫЖЏЪБЃЌЕуPдкyжсЩЯЕФЮЛжУЪЧЗёЗЂЩњИФБфЃЌЮЊЪВУДЃП
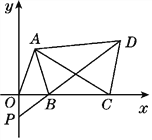
ЁОД№АИЁПЃЈ1ЃЉЯрЕШЃЛЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3)ЮЛжУВЛЗЂЩњИФБф
ЁОНтЮіЁПЪдЬтЗжЮіЃК ![]() ЯШИљОнЗЧИКЪ§ЕФаджЪЧѓГі
ЯШИљОнЗЧИКЪ§ЕФаджЪЧѓГі![]() ЕФжЕЃЌзї
ЕФжЕЃЌзї![]() гкЕу
гкЕу![]() ЃЌгЩ
ЃЌгЩ![]() ЖЈРэЕУГі
ЖЈРэЕУГі![]() ИљОнШЋЕШШ§НЧаЮЕФаджЪМДПЩЕУГіНсТл.
ИљОнШЋЕШШ§НЧаЮЕФаджЪМДПЩЕУГіНсТл.![]() ЯШИљОн
ЯШИљОн![]() ЕУГі
ЕУГі![]() дйгЩ
дйгЩ![]() ЖЈРэМДПЩЕУГі
ЖЈРэМДПЩЕУГі![]()
![]() Щш
Щш![]() гЩШЋЕШШ§НЧаЮЕФаджЪПЩЕУГі
гЩШЋЕШШ§НЧаЮЕФаджЪПЩЕУГі![]() ЙЪ
ЙЪ![]() ЮЊЖЈжЕЃЌдйгЩ
ЮЊЖЈжЕЃЌдйгЩ![]() ПЩжЊ
ПЩжЊ![]() ЕФГЄЖШВЛБфЃЌЙЪПЩЕУГіНсТлЃЎ
ЕФГЄЖШВЛБфЃЌЙЪПЩЕУГіНсТлЃЎ
ЪдЬтНтЮіЃК
![]() жЄУїЃК
жЄУїЃК![]()
![]() НтЕУ
НтЕУ![]()
![]()
зї![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ
![]()
![]()
дк![]() гы
гы![]() жаЃЌ
жаЃЌ
![]()
![]()
![]() жЄУїЃК
жЄУїЃК ![]()
![]()
МД![]()
дк![]() гы
гы![]() жаЃЌ
жаЃЌ
![]()
![]() Еу
Еу![]() дк
дк![]() жсЩЯЕФЮЛжУВЛЗЂЩњИФБф.
жсЩЯЕФЮЛжУВЛЗЂЩњИФБф.
РэгЩЃКЩш![]()
ЁпгЩ![]() жЊ
жЊ![]()
![]()
![]() ЮЊЖЈжЕ,
ЮЊЖЈжЕ,
![]()
Ёр![]() ГЄЖШВЛБфЃЌ
ГЄЖШВЛБфЃЌ
Еу![]() дк
дк![]() жсЩЯЕФЮЛжУВЛЗЂЩњИФБф.
жсЩЯЕФЮЛжУВЛЗЂЩњИФБф.


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
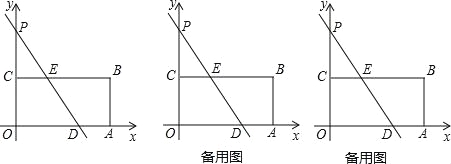
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЫФБпаЮOABCЮЊОиаЮЃЌЕуAЁЂBЕФзјБъЗжБ№ЮЊЃЈ12ЃЌ0ЃЉЁЂЃЈ12ЃЌ6ЃЉЃЌжБЯпy=Љ![]() x+bгыyжсНЛгкЕуPЃЌгыБпOAНЛгкЕуDЃЌгыБпBCНЛгкЕуEЃЎ
x+bгыyжсНЛгкЕуPЃЌгыБпOAНЛгкЕуDЃЌгыБпBCНЛгкЕуEЃЎ
ЃЈ1ЃЉШєжБЯпy=Љ![]() x+bЦНЗжОиаЮOABCЕФУцЛ§ЃЌЧѓbЕФжЕЃЛ
x+bЦНЗжОиаЮOABCЕФУцЛ§ЃЌЧѓbЕФжЕЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЕБжБЯпy=Љ![]() x+bШЦЕуPЫГЪБеыа§зЊЪБЃЌгыжБЯпBCКЭxжсЗжБ№НЛгкЕуNЁЂMЃЌЮЪЃКЪЧЗёДцдкONЦНЗжЁЯCNMЕФЧщПіЃПШєДцдкЃЌЧѓЯпЖЮDMЕФГЄЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
x+bШЦЕуPЫГЪБеыа§зЊЪБЃЌгыжБЯпBCКЭxжсЗжБ№НЛгкЕуNЁЂMЃЌЮЪЃКЪЧЗёДцдкONЦНЗжЁЯCNMЕФЧщПіЃПШєДцдкЃЌЧѓЯпЖЮDMЕФГЄЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌНЋОиаЮOABCбиDEелЕўЃЌШєЕуOТфдкБпBCЩЯЃЌЧѓГіИУЕузјБъЃЛШєВЛдкБпBCЩЯЃЌЧѓНЋЃЈ1ЃЉжаЕФжБЯпбиyжсдѕбљЦНвЦЃЌЪЙОиаЮOABCбиЦНвЦКѓЕФжБЯпелЕўЃЌЕуOЧЁКУТфдкБпBCЩЯЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
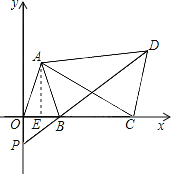
ЁОЬтФПЁПШчЭМЫљЪОЃЌ AB=ACЃЌAD=AEЃЌЁЯBAC=ЁЯDAEЃЌЁЯ1=25ЁуЃЌЁЯ2=30ЁуЃЌдђЁЯ3=_____.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁїABCжаЃЌAB=AC=4ЃЌЁЯA=60ЁуЃЌдђЁїABCЕФжмГЄЮЊ______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉвЛЬѕжБЯпПЩвдАбЦНУцЗжГЩСНИіВПЗжЃЈЛђЧјгђЃЉЃЌШчЭМЃЌСНЬѕжБЯпПЩвдАбЦНУцЗжГЩМИИіВПЗжЃПШ§ЬѕжБЯпПЩвдАбЦНУцЗжГЩМИИіВПЗжЃПЪдЛЭМЫЕУїЃЎ

ЃЈ2ЃЉЫФЬѕжБЯпзюЖрПЩвдАбЦНУцЗжГЩМИИіВПЗжЃПЪдЛГіЪОвтЭМЃЌВЂЫЕУїетЫФЬѕжБЯпЕФЮЛжУЙиЯЕЃЎ
ЃЈ3ЃЉЦНУцЩЯга![]() ЬѕжБЯпЃЌУПСНЬѕжБЯпЖМЧЁКУЯрНЛЃЌЧвУЛгаШ§ЬѕжБЯпНЛгквЛЕуЃЌДІгкетжжЮЛжУЕФ
ЬѕжБЯпЃЌУПСНЬѕжБЯпЖМЧЁКУЯрНЛЃЌЧвУЛгаШ§ЬѕжБЯпНЛгквЛЕуЃЌДІгкетжжЮЛжУЕФ![]() ЬѕжБЯпЗжвЛИіЦНУцЫљГЩЕФЧјгђзюЖрЃЌМЧЮЊ
ЬѕжБЯпЗжвЛИіЦНУцЫљГЩЕФЧјгђзюЖрЃЌМЧЮЊ![]() ЃЌЪдбаОП
ЃЌЪдбаОП![]() гы
гы![]() жЎМфЕФЙиЯЕЃЎ
жЎМфЕФЙиЯЕЃЎ
ЫМЮЌЗНЗЈЬьЕи
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌEЪЧBCБпЩЯвЛЕуЃЌABЁЭBCгкЕуBЃЌDCЁЭBCгкЕуCЃЌABЃНBCЃЌЁЯAЃНЁЯCBDЃЌAEгыBDНЛгкЕуOЃЌгаЯТСаНсТлЃКЂйAEЃНBDЃЛЂкAEЁЭBDЃЛЂлBEЃНCDЃЛЂмЁїAOBЕФУцЛ§ЕШгкЫФБпаЮCDOEЕФУцЛ§ЃЎЦфжае§ШЗЕФНсТлга( )
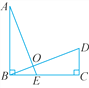
A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП
вЛИіе§ЗНаЮЕФУцЛ§ЪЧ6ЦНЗНРхУзЃЌдђетИіе§ЗНаЮЕФБпГЄЕШгкРхУзЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
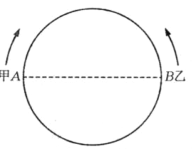
ЁОЬтФПЁПФГаЃЮЊХрбјЧрЩйФъПЦММДДаТФмСІЃЌОйАьСЫЖЏТўжЦзїЛюЖЏЃЌаЁУїЩшМЦСЫЕузідВжмдЫЖЏЕФвЛИіГћаЭ.ШчЭМЫљЪОЃЌМзЁЂввСНЕуЗжБ№ДгжБОЖЕФСНЖЫЕу AЁЂBвдЫГЪБеыЁЂФцЪБеыЕФЗНЯђЭЌЪБбидВжмдЫЖЏ. МздЫЖЏЕФТЗГЬl(cm)гыЪБМфt(s)ТњзуЙиЯЕЃК![]() (tЁн0)ЃЌвввд4 cm/sЕФЫйЖШдШЫйдЫЖЏЃЌАыдВЕФГЄЖШЮЊ 21 cm.
(tЁн0)ЃЌвввд4 cm/sЕФЫйЖШдШЫйдЫЖЏЃЌАыдВЕФГЄЖШЮЊ 21 cm.
(1)МздЫЖЏ 4 sКѓЕФТЗГЬЪЧЖрЩйЃП
(2)МзЁЂввДгПЊЪМдЫЖЏЕНЕквЛДЮЯргіЪБЃЌЫќУЧдЫЖЏСЫЖрЩйЪБМфЃП
(3)МзЁЂввДгПЊЪМдЫЖЏЕНЕкЖўДЮЯргіЪБЃЌЫќУЧдЫЖЏСЫЖрЩйЪБМфЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
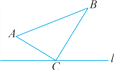
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACBЃН90ЁуЃЌACЃН6ЃЌBCЃН8.ЕуPДгЕуAГіЗЂбиТЗОЖAЁњCЁњBЯђжеЕуBдЫЖЏЃЛЕуQДгЕуBГіЗЂбиТЗОЖBЁњCЁњAЯђжеЕуAдЫЖЏЃЎЕуPКЭЕуQЗжБ№вд1ИіЕЅЮЛ/УыКЭ3ИіЕЅЮЛ/УыЕФЫйЖШЭЌЪБПЊЪМдЫЖЏЃЌСНЕуЖМвЊЕНЯргІЕФжеЕуЪБВХФмЭЃжЙдЫЖЏЃЌдкФГвЛЪБПЬЃЌЙ§ЕуPзїPEЁЭlгкЕуEЃЌЙ§ЕуQзїQFЁЭlгкЕуF.ЮЪЃКЕуPдЫЖЏЖрЩйЪБМфЪБЃЌЁїPECгыЁїCFQШЋЕШЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com