
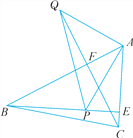
【题目】如图,已知在△ABC中,AB>AC,BE,CF都是△ABC的高线,P是BE上一点,且BP=AC,Q是CF延长线上一点,且CQ=AB,连结AP,AQ,QP.求证:
(1)AQ=PA.
(2)AP⊥AQ.
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:(1)由已知条件可求出∠ABP=∠QCA,即可根据SAS证得△AQC≌△PAB(SAS),就可以得出AP=AQ;
(2)根据全等三角形的性质,由△AQC≌△PAB可得出∠BAP=∠CQA,再由∠CQA+∠FAQ=90°,即可证明.
试题解析:(1)∵BE,CF是△ABC的高线,
∴BE⊥AC,CF⊥AB,
∴∠ABP+∠BAC=∠ACQ+∠BAC=90°,
∴∠ABP=∠ACQ.
在△AQC和△PAB中,∵ 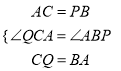
∴△AQC≌△PAB(SAS).∴AQ=PA.
(2)∵△AQC≌△PAB,∴∠BAP=∠CQA.
∵∠CQA+∠BAQ=90°,
∴∠BAP+∠BAQ=90°,∴AP⊥AQ.


科目:初中数学 来源: 题型:
【题目】如图,E是BC边上一点,AB⊥BC于点B,DC⊥BC于点C,AB=BC,∠A=∠CBD,AE与BD交于点O,有下列结论:①AE=BD;②AE⊥BD;③BE=CD;④△AOB的面积等于四边形CDOE的面积.其中正确的结论有( )
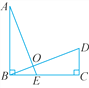
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)交x轴于A(﹣1,0),B(5,0)两点,与y轴交于点C(0,2)
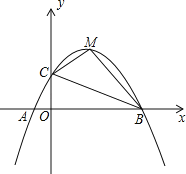
(1)求抛物线的解析式;
(2)若点M为抛物线的顶点,连接BC、CM、BM,求△BCM的面积;
(3)连接AC,在x轴上是否存在点P使△ACP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“故人西辞黄鹤楼,烟花三月下扬州”,据报道去年扬州旅游总收入近900亿元,大部分的旅游收入是靠“皮包骨“的湖泊﹣﹣瘦西湖得来.将数据90000000000用科学记数法表示为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
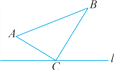
【题目】如图,在△ABC中,∠ACB=90°,AC=6,BC=8.点P从点A出发沿路径A→C→B向终点B运动;点Q从点B出发沿路径B→C→A向终点A运动.点P和点Q分别以1个单位/秒和3个单位/秒的速度同时开始运动,两点都要到相应的终点时才能停止运动,在某一时刻,过点P作PE⊥l于点E,过点Q作QF⊥l于点F.问:点P运动多少时间时,△PEC与△CFQ全等?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级(2)班派出12名同学参加数学竞赛,老师以75分为基准,把分数超过75分的部分记为正数,不足的部分记为负数.评分记录如下:
+15,+20,-5,-4,-3,+4,+6,+2,+3,+5,+7,-8
(1)这12名同学中最高分和最低分各是多少分?
(2)超过基准分的有多少人?
(3)这12名同学的平均成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
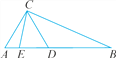
【题目】如图,在△ABC中,AD=AC,BE=BC.
(1)若∠ACB=96°,求∠DCE的度数.
(2)问:∠DCE与∠A,∠B之间存在怎样的数量关系(直接写出答案)?
查看答案和解析>>
科目:初中数学 来源: 题型:
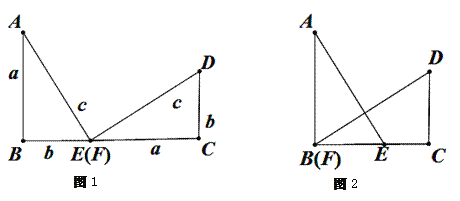
【题目】(1)以a,b为直角边,c为斜边作两个全等的Rt△ABE与Rt△FCD拼成如图1所示的图形,使B,E,F,C四点在一条直线上(此时E,F重合),可知△ABE ≌△FCD,AE![]() DF,请你证明:
DF,请你证明:![]() ;
;
(2)在(1)中,固定△FCD,再将△ABE沿着BC平移到如图2的位置(此时B,F重合),请你重新证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com