
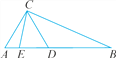
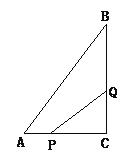
【题目】如图,在△ABC中,AD=AC,BE=BC.
(1)若∠ACB=96°,求∠DCE的度数.
(2)问:∠DCE与∠A,∠B之间存在怎样的数量关系(直接写出答案)?
【答案】(1)42°(2)∠DCE=![]() (∠A+∠B)
(∠A+∠B)
【解析】试题分析:(1)先由等边对等角的性质和三角形内角和定理得出∠A,∠B,∠ACB+∠A+∠B,然后等量代换求出∠DCE;
(2)由(1)可知∠DCE=180°-(∠CED+∠CDE),再由∠A=180°-2∠CDE,∠B=180°-2∠CED,得出∠1=90°-![]() ∠B,∠2=90°-
∠B,∠2=90°-![]() ∠A,将它们代入即可得出∠DCE=
∠A,将它们代入即可得出∠DCE=![]() (∠A+∠B),即可得到∠A,∠B与∠DCE之间的数量关系.
(∠A+∠B),即可得到∠A,∠B与∠DCE之间的数量关系.
试题解析:(1)∵AD=AC,
∴∠ADC=∠ACD.
∴∠A=180°-2∠ADC.
∵BE=BC,
∴∠CEB=∠ECB.
∴∠B=180°-2∠CEB.
∵∠ACB=96°,∴∠A+∠B=84°.
∴(180°-2∠ADC)+(180°-2∠CEB)=84°.
∴∠CEB+∠ADC=138°.∴∠DCE=42°.
(2)∠DCE=![]() (∠A+∠B).
(∠A+∠B).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
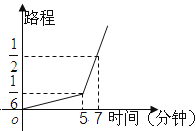
【题目】一名考生步行前往考场,5分钟走了总路程的![]() ,估计步行不能准时到达,于是他改乘出租车赶往考场,他的行程与时间关系如图所示(假定总路程为1,出租车匀速),则他到达考场所花的时间比一直步行提前了________分钟。
,估计步行不能准时到达,于是他改乘出租车赶往考场,他的行程与时间关系如图所示(假定总路程为1,出租车匀速),则他到达考场所花的时间比一直步行提前了________分钟。
查看答案和解析>>
科目:初中数学 来源: 题型:
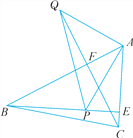
【题目】如图,已知在△ABC中,AB>AC,BE,CF都是△ABC的高线,P是BE上一点,且BP=AC,Q是CF延长线上一点,且CQ=AB,连结AP,AQ,QP.求证:
(1)AQ=PA.
(2)AP⊥AQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
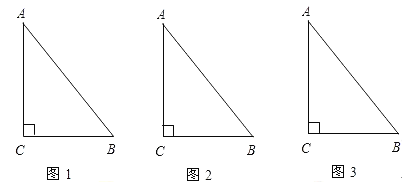
【题目】某园艺公司对一块直角三角形的花圃进行改造.测得两直角边长为6m、8m.现要将其扩建成等腰三角形,且扩充部分是以8m为直角边的直角三角形.求扩建后的等腰三角形花圃的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂从生产的袋装食品中抽出样品8袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:

(1)这8袋样品的总质量比标准质量多还是少?多或少几克?
(2)若标准质量为500克,则抽样检测这8袋的总质量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图4所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
(1)、如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8平方厘米?
(2)、点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于△ABC的面积的一半.若存在,求出运动的时间;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com