
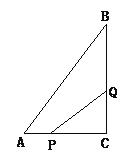
【题目】如图4所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
(1)、如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8平方厘米?
(2)、点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于△ABC的面积的一半.若存在,求出运动的时间;若不存在,说明理由.
【答案】(1)、2s或4s;(2)、不存在
【解析】
试题分析:(1)设时间为x,则分别用含x的代数式表示PC和CQ的长度,根据三角形面积的计算公式求出x的值;(2)、方法同第一个.
试题解析:(1)设xs后,可使△PCQ的面积为8![]() ,所以 AP=xcm,PC=(6-x)cm,CQ=2xcm.
,所以 AP=xcm,PC=(6-x)cm,CQ=2xcm.
则根据题意,得![]() ·(6-x)·2x=8.整理,得
·(6-x)·2x=8.整理,得![]() -6x+8=0
-6x+8=0
解得![]() =2,
=2,![]() =4.
=4.
所以P、Q同时出发,2s或4s后可使△PCQ的面积为8![]() .
.
(2)、设点P出发x秒后,△PCQ的面积等于△ABC面积的一半.
则根据题意,得![]() (6-x)·2x=
(6-x)·2x=![]() ×
×![]() ×6×8.整理,得
×6×8.整理,得![]() -6x+12=0.
-6x+12=0.
由于此方程没有实数根,所以不存在使△PCQ的面积等于△ABC面积一半的时刻.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)交x轴于A(﹣1,0),B(5,0)两点,与y轴交于点C(0,2)
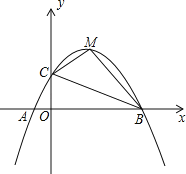
(1)求抛物线的解析式;
(2)若点M为抛物线的顶点,连接BC、CM、BM,求△BCM的面积;
(3)连接AC,在x轴上是否存在点P使△ACP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级(2)班派出12名同学参加数学竞赛,老师以75分为基准,把分数超过75分的部分记为正数,不足的部分记为负数.评分记录如下:
+15,+20,-5,-4,-3,+4,+6,+2,+3,+5,+7,-8
(1)这12名同学中最高分和最低分各是多少分?
(2)超过基准分的有多少人?
(3)这12名同学的平均成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
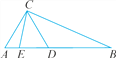
【题目】如图,在△ABC中,AD=AC,BE=BC.
(1)若∠ACB=96°,求∠DCE的度数.
(2)问:∠DCE与∠A,∠B之间存在怎样的数量关系(直接写出答案)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是由一些火柴棒搭成的图案:
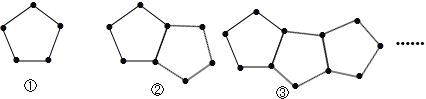
(1)摆第①个图案用 根火柴棒,摆第②个图案用 根火柴棒,摆第③个图案用 根火柴棒.
(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒?
(3)计算一下摆121根火柴棒时,是第几个图案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备食建一个面积为200m2的矩形花圃,它的长比宽多10m,设花圃的宽为x m.则可列方程为( )
A.x (x﹣10)=200
B.2x+2 (x﹣10)=200
C.x(x+10)=200
D.2x+2(x+10)=200
查看答案和解析>>
科目:初中数学 来源: 题型:
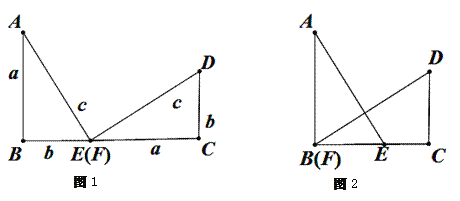
【题目】(1)以a,b为直角边,c为斜边作两个全等的Rt△ABE与Rt△FCD拼成如图1所示的图形,使B,E,F,C四点在一条直线上(此时E,F重合),可知△ABE ≌△FCD,AE![]() DF,请你证明:
DF,请你证明:![]() ;
;
(2)在(1)中,固定△FCD,再将△ABE沿着BC平移到如图2的位置(此时B,F重合),请你重新证明:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郑州市雾霾天气趋于严重,丹尼斯商场根据民众健康需要,代理销售每台 进价分别为600元、560元的A、B两种型号的空气净化器,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 4台 | 5台 | 7100元 |
第二周 | 6台 | 10台 | 12600元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A,B两种型号的空气净化器的销售单价;
(2)若商场准备用不多于17200元的金额再采购这两种型号的空气净化器共30台,超市销售完这30台空气净化器能否实现利润为6200元的目标,若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com